Proszę o pomoc Martyna: Proszę o pomoc Stosunek długości przekątnych rombu jest równy 2 : 3. Znajdź stosunek długości boku tego rombu do długości promienia koła wpisanego w ten rom

wredulus_pospolitus: z zależności pomiędzy okręgiem wpisanym w czworokąt a tymże czworokątem mamy:

	2P▱		d1*d2
r =		=
	4a		4a

przyjmijmy sobie pomocniczą jednostkę 'b' taką, że: d₁ = 4b ; d₂ = 6b jeżeli narysujesz sobie romb, przekątne ... to zauważysz trójkąt prostokątny o

	d1		d2
przyprostokątnych		,		oraz przeciwprostokątnej a
	2		2

Z tw. Pitagorasa: (2b)² + (3b)² = a² −−−> a² = 13b² −−−> a = √13b Wracamy do początkowego wzoru:

	d1*d2		4b*6b		6b
r =		=		=
	4a		4√13b		√13

	a		6b		13
więc		= U{√13b}{		=		więc masz stosunek 13 : 6.
	r		√13		6

Jolanta:

	e*f
P=
	2

e=2x. f=3x

	2x*3x
P=		=3x2
	2

P=a*h=a*2r 3x²=2ar

	1		1
(		e)2+(		f)2=a2
	2		2

	2x		3x
(		)2+(		)2=a2
	2		2

	9
x2+		x2=a2
	4

13
	x2=a2
4

	4a2
x2=
	13

	4a2
3(		)=2ar /: a
	13

12a
	=2r
13

12a=26r

a		13
	=
r		6

Jolanta: Najlepiej zrobić rysunek Wykorzystałam wzory na pole rombu z przekątnymi i bok razy wysokość A później z tw Pitagorasa Trójkąt prostokątny o bokach a ,1/2e ,1/2f

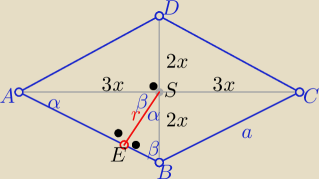
rąbek: Prawie bez obliczeń: Z podobieństwa trójkątów AES i BES z cechy (kkk)

	3
w skali k=
	2

	3		2		13
|AE| =		r i |BE|=		r to |AB|=a=		r
	2		3		6

zatem:

	a		13
		=
	r		6

i po ptokach

ząbek: