graniastosłup prawidłowy trójkątny o krawędzi podstawy a przecięto płaszczyzną p
mat: graniastosłup prawidłowy trójkątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą
przez przekątną ściany bocznej i środek tej krawędzi podstawy która nie ma punktu wspólnego z
tą przekątną. Pole otrzymanego przekroju jest równe S. Oblicz cosinus kata, który płaszczyzna
przekroju tworzy z dolną podstawą oraz wyznacz objętość tego graniastosłupa.
15 gru 20:15
.:
No dobrze.
Na jakim etapie się zatrzymałeś? Rysunek zrobiony? Jeżeli tak to jak wygląda.
Kąt zaznaczony? Pokaż.
15 gru 20:42
mat: n nie wiem od czego zacząć
15 gru 20:43
.:
Zacznij od rysunku i zaznaczenia przekroju.
Pokaz co narysowałeś i pójdziemy z tym dalej.
Bez tego 'ani rusz'
15 gru 20:48
mat:
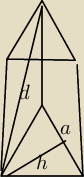
15 gru 20:48
wredulus_pospolitus:
dokończ ten przekrój jak z górnego wierzchołka będziemy 'schodzić' do środka dolnej krawędzi?
2. zaznacza KĄT pomiędzy podstawą na tą właśnie płaszczyzną
15 gru 20:55
mat: pole podstawy 〖√3 a〗2/4
wysokość h to (√3 a)/2
15 gru 20:55
wredulus_pospolitus:
3. jaką figurę daje tworzy nam ten przekrój
konkretnie −−− jaka to figura
15 gru 20:57
wredulus_pospolitus:
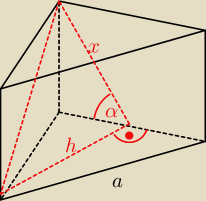
15 gru 21:01
mat:
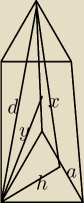
15 gru 21:02
mat: przekrój to trójkąt i wydaje mi się że równoramienny
15 gru 21:04
mat: przekrój to nie trójkąt równoramienny bo przekątna ściany to nie jest równa x
15 gru 21:11
szach mat:
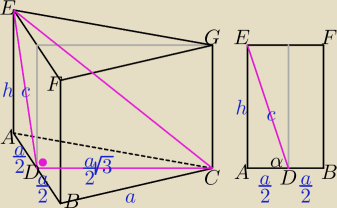
| | 1 | | a | |
Pole trójkąta DCE: |
| * |
| √3 * c = S stąd c = ... |
| | 2 | | 2 | |
h z twierdzenia Pitagorasa w trójkącie ADE: h =
√ c2 − (a/2)2
| | 1 | |
Objętość V = |
| a2√3 * h |
| | 4 | |
15 gru 21:33
wredulus_pospolitus:
mat −−− przekrój jest trójkątem PROSTOKĄTNYM i po prostu jedną z przyprostokątnych nazwałem 'x'
15 gru 21:55