szachownica Grandecojones: Na kazdym polu szachownicy o wymiarach 6 × 6 ustawiono do kładnie jeden pionek − bialy lub czarny. Okazalo sie, ze rozmieszczono tyle samo pionkow bialych, co czarnych, a w kazdym kwadracie o wymiarach 2 × 2 znajduje sie co najmniej jeden pionek kazdego koloru. Udowodnij, ze w pewnym kwadracie o wymiarach 2 × 2 znajduja sie dokładnie dwa pionki biale i dwa czarne. Wysłano

wredulus_pospolitus: Z jakiego konkursu jest to zadanie

Grandecojones: sprawdzian predyspozycji do klas matematycznych liceum staszica w warszawie

wredulus_pospolitus: Z którego roku ?

Grandecojones:

wredulus_pospolitus: Oki ... wskazówka: Zauważ, że szachownice 6x6 można podzielić na 9 nienakładających się kwadratów 2x2. Miej na uwadze, że liczba pionów każdego koloru jest taka sama i wynosi 18.

Grandecojones: juz dawno rozwiazane, dzieki. Ale podpowiedz poprawna !

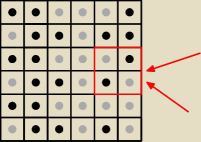
wredulus_pospolitus: To tak naprawdę jest 'za mało' aby wykazać, że tak jest (jak na razie wykazujemy, że szachownicę tą nie można zapełnić 18 białymi i 18 czarnymi pionami tak aby w każdym kwadracie było tylko 1B+3Cz lub 3B+1Cz). Ale widząc to rozwiązanie możesz odpowiednio podać przykład szachownicy podzielonej tak, że żaden z kwadratów nie ma 4x Cz lub 4xB i dokładnie 1 kwadra 2xB i 2x Cz (co pokazuje że taki układ na szachownicy w ogóle jest możliwy ... a to w połączeniu z wcześniejszym pokazuje, że jeżeli mamy układ 'brak 4x tego samego koloru i taka sama liczba pionów' to mamy przynajmniej jeden kwadracik 2B i 2Cz) i to (moim zdaniem) dopiero jest pełnym dowodem / wykazaniem.