Prawdopodobienstwo calkowite
matematycznyswir: Z urny zawierającej 6 kul białych i 4 czarne losujemy kulę x i nie oglądając jej, wkładamy do
drugiej urny, w której początkowo było 7 kul czarnych i 4 białe. Następnie z drugiej urny
losujemy jednocześnie dwie kule. Oblicz prawdopodobieństwo, że będą one rożnego koloru.
Mam problem z tego typu zadaniami, ponieważ wydaje się zbyt skomplikowane na rozwiązanie metodą
drzewka, która jednak jest dla mnie najbardziej intuicyjna. Jaki jest najprostszy sposób na
to?
8 gru 13:50
wredulus_pospolitus:
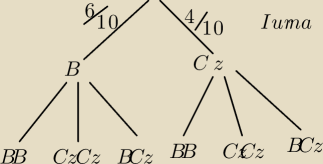
Dla ułatwienia możesz spróbować je rozwiązać za pomocą drzewka (nim nie 'złapiesz' idei).
Prawdopodobieństwa w II urnie na drzewko to będzie odpowiednio:
| | 5*4 | | 7*6 | | 2*7*5 | |
BB: |
| ; CzCz = |
| ; BCz = |
| |
| | 12*11 | | 12*11 | | 12*11 | |
| | 4*3 | | 8*7 | | 2*8*4 | |
BB: |
| ; CzCz = |
| ; BCz = |
| |
| | 12*11 | | 12*11 | | 12*11 | |
| | 6 | | 2*7*5 | | 4 | | 2*8*4 | |
P(A) = |
| * |
| + |
| * |
| |
| | 10 | | 12*11 | | 10 | | 12*11 | |
8 gru 15:41
wredulus_pospolitus:
Po prostu musisz załapać:
Jaka będzie sytuacja w II urnie gdy z I urny ... wylosowano Białą ... wylosowano Czarną
8 gru 15:42