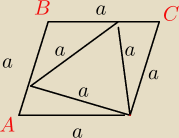
 Oblicz miarę kąta ABC
Oblicz miarę kąta ABC
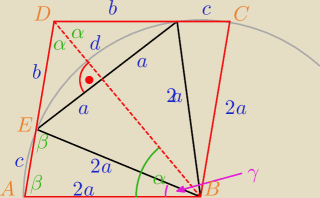 Jeden ze sposobów (kąty trójkątów równoramienny):
0. ABCD jest rombem
Jeden ze sposobów (kąty trójkątów równoramienny):
0. ABCD jest rombem  (skąd to wiem ?)
1. Rysunek
2. Zamieniłem długość boku z 'a' na '2a', bo nie chciałem mieć ułamka.
3. z trójkąta równoramiennego ABE
γ = α − 30o = 180o − 2β −−−> α = 210o − 2β
4. z trójkąta równoramiennego ABD
β = 180o − 2α = 180o − 2*(210o − 2β) −−−> 3β = 420o − 180o −−−> β = 80o
4. ABCD jest rombem ... związku z tym ∡ADC = 180o − 80o = 100o
(skąd to wiem ?)
1. Rysunek
2. Zamieniłem długość boku z 'a' na '2a', bo nie chciałem mieć ułamka.
3. z trójkąta równoramiennego ABE
γ = α − 30o = 180o − 2β −−−> α = 210o − 2β
4. z trójkąta równoramiennego ABD
β = 180o − 2α = 180o − 2*(210o − 2β) −−−> 3β = 420o − 180o −−−> β = 80o
4. ABCD jest rombem ... związku z tym ∡ADC = 180o − 80o = 100o
 Notatka −−− większość oznaczeń okazała się niepotrzebna (początkowo chciałem inaczej podejść do
tego zadania ... męczyć się z układem równań z tw. cosinusów i trygonometrycznych)
Notatka −−− większość oznaczeń okazała się niepotrzebna (początkowo chciałem inaczej podejść do
tego zadania ... męczyć się z układem równań z tw. cosinusów i trygonometrycznych)
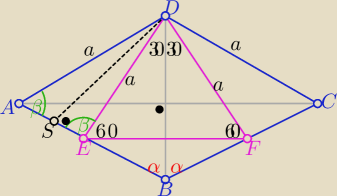 β kąt zewnętrzny ΔBED i kąt ostry rombu
to β= 30o+α
więc β+2α=180o ⇒ 30o+α+2α=180o ⇒ α=50o
to |∡ABC|=2α= 100o
i po ptokach
β kąt zewnętrzny ΔBED i kąt ostry rombu
to β= 30o+α
więc β+2α=180o ⇒ 30o+α+2α=180o ⇒ α=50o
to |∡ABC|=2α= 100o
i po ptokach 