Równanie (x,y) #k: Zadanie nr 24 Dane jest równanie x(y+1)*(x+y²+y)+y⁴+y³=0 a) Dla jakich wartości parametru y dane równanie ma dwa rózne rozwiązania ujemne ? b)^* Narysuj w układzie współrzdnych figurę opisana danym równaniem i na podstawie otrzymanego wykresu określ liczbe rozwiązań danego równania w zależności od 1) parametru y gdy x jest niewiadomą 2) parametru x gdy y jest niewiadomą Podpunkt a) jest stosunkowo łatwy do zrobienia Równanie bedzie miało postac x²(y+1)+x(y³+2y²+y)+y⁴+y³=0 Warunki 1)Δ>0 1)x₁*x₂>0 Jeśli chodzi o podpunkt b) Należy to równanie doprowadzic do postaci (y+1)(x+y)(x+y²)=0 Tutaj bym prosił o pomoc . Dziękuje

chichi: x²(y + 1) + (y³ + 2y² + y)x + y⁴ + y³ = 0 x²(y + 1) + y(y² + 2y + 1) + y³(y + 1) = 0 x² + y(y + 1)²x + y³(y + 1) = 0 (y + 1)(x² + y(y + 1)x + y³) = 0 no i teraz rozkład trójmianu z drugiego nawiasu zależy od twojego sprytu. bez wysiłkowo można to zrobić wprost korzystając z wyróżnika trójmianu kwadratowego, dasz radę?

chichi: w trzecim wierszu zjadłem (y + 1) przy x², sorki

#k: Na razie dziękuje Bede próbowal ale juz rano

chichi: a tak á propos tego podpunktu (a) to jeszcze warunek x₁ + x₂ < 0 by się przydał

#k: Wezme tez ten warunek pod uwagę .

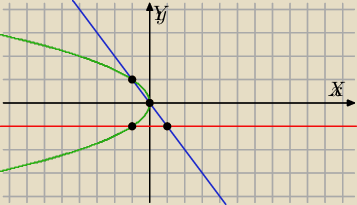
#k: Mam wtedy do podpunktu b) (y+1)(x+y)(x+y²)=0 Wtedy jest prosta y=−1 (czerwona prosta y=−x (niebieska parabola x=−y² (zielona 1^o Dla y=0 i y=1 równanie to ma jedno rozwiązanie Dla y∊(−∞,∞)\{−1,0,1} równanie to ma dwa rozwiązania Dla y=−1 równanie to ma nieskończenie wiele rozwiązan 2^o Dla x=1 równanie to ma jedno rozwiązanie Dla x∊[0,1)U(1,∞)U{−1} równanie to ma dwa rozwiązania Dla x∊(−∞−1)U(−1,0) równanie to ma cztery rozwiązania Czy rysunek i rozwiązania są dobre ? dziękuje