Problem optymalizacyjny rzeczywisty
cienkistudent:
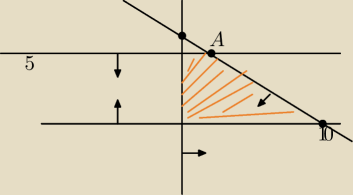
Max z = 20x + 50y
| ⎧ | 2x+3y≤20 | |
| ⎨ | y≤5 |
|
| ⎩ | x,y≥0 ∍ Z | |
Doszedłem do wniosku A(2,5 ; 5)
Z(A) = 300
Ale tą muszą być całkowite więc 2,5 odpada. Jak to rozwiązać ?
1 gru 14:26
wredulus_pospolitus:
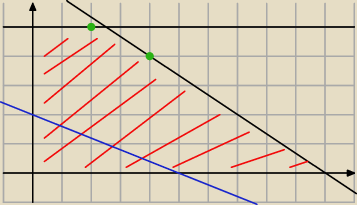
graficznie:
1. rysujesz obszar
| | −2x+c | |
2. rysujesz g(x) = |
| na rysunku c = 10 |
| | 5 | |
3. bierzesz do łapki dwie ekierki lub ekierkę i linijkę i przesuwasz równolegle prostą tak
długo aż dojdziesz do DRUGIEGO z zielonych punktów ... to jest punkt który zwraca Ci
maksymalna wartość wyrażenia przy całkowitych wartościach (x,y)
1 gru 14:40
cienkistudent: Okej, a skąd to g(x) = −2x+c/5 ?
1 gru 14:53
wredulus_pospolitus:
nie −2x+c/5 tylko (−2x+c)/5
| | −2x + c | |
z: zmax = 20x + 50y −−−> 50y = −20x + zmax −−−> y = |
| gdzie 'c' to |
| | 5 | |
nieznana nam stała
więc ... przyjmuję sobie 'jakąś' wartość dla c, aby narysować prostą (niebieska) ... następnie
przesuwając równolegle otrzymuję inne proste które reprezentują inną wartość 'c' (zauważ, że
c
max jest powiązane z szukanym z
max −−> 10*c
max = z
max)
1 gru 14:58
cienkistudent: Okej rozumiem,ostatnie 2 krótkie pytania. Gdyby chodziło tu o Rzeczywiste to punktem
rozwiązania byłby punkt A
który zaznaczyłem w swoim wykresie? Bo przecież maksymalizacja to ostatnia styczna ?
A gdyby chodziło o minimalizacje na tym samym przykładzie to rozwiązaniem byłby ten PIERWSZY
punkt na twoim wykresie?
1 gru 15:17
.:
Tak i tak.
Oczywiście mam nimalna wartością w tym przypadku byłoby 0

1 gru 15:20
 Max z = 20x + 50y
Max z = 20x + 50y
 graficznie:
1. rysujesz obszar
graficznie:
1. rysujesz obszar
