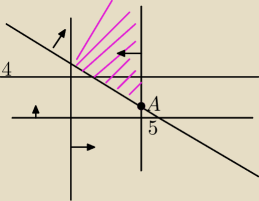
Rozwiąż graficznie problem optymalistyczny rzeczywisty cienkistudent: Rozwiąż graficznie problem optymalistyczny rzeczywisty Min z = 2x1+ 4x2 x1 + x2 >=6 x1 <=5 x2 = 4 x1, x2 >=0 i należą do R Wziąłem funkcję celu 2x1 + 4x2 = 12 wyszły punkty (0,3) (6,0) Z tego wziąłem A(5,1) i Z(A) = 14 (bo schodze z nią w dół) Dobrze czy coś źle, jeżeli źle robie z tą funkcją celu może ktoś wyjaśnic?

grubystudent: Co to jest problem optymalistyczny?

cienkistudent: Nie wiem, ale jak nie masz nic ciekawszego do powiedzenia to nie musisz się mądrzyć

cienkistudent: chodzi o optymalizacyjny

grubystudent: Czy pisząc znak >= chodziło Ci o znak ≥, jest tuż nad polem tekstowym, między znakami ≤ i ∊. Zagadnienia optymalizacyjne znam, ale optymalistycznych nie znam i dlatego zapytałem

grubystudent: i ostatnie pytanie cienkistudencie, czy 2x1+ 4x2 i podobne inne Twoje zapisy to 2x₁ + 4x₂?

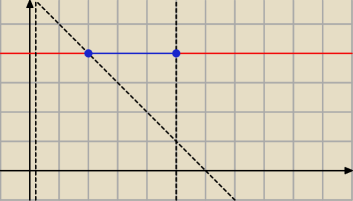
wredulus_pospolitus: keee niebieski odcinek to zbiór który spełnia warunki do optymalizacji z = 2x₁ + 4x₂ = 2x₁ + 4*4 = 2x₁ + 16 z_min = 2*2 + 16 = 20

cienkistudent: Nie czaje dlaczego ten odcinek to zbiór który spełnia warunki? Albo kiedy odcinek jest zbiorem kiedy spełnia warunki do optymalizacji?

wredulus_pospolitus: napisałeś warunek: "x₂ = 4"

wredulus_pospolitus: jeżeli miało być x₂ ≤ 4 to obszarem będzie trójkąt i wtedy robisz analogicznie do tego dzisiejszego zadania:

	1
zmin = 2x1 + 4x2 −−−> x2 = −		x1 + c ; gdzie c to 'jakaś stała' ... rysujesz
	2

prostą i przesuwasz równolegle 'w górę' lub 'w dół' aż złapiesz punkt z przedziału