proszę o rozwiązanie anna: udowodnij że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x⁴ − 4x³ − 2x² + 12x +9 ≥ 0

anna: dziękuję już zrobiłam korzystałam ze schematu Hornera

wredulus_pospolitus: 1. zauważmy że dla f(x) = x⁴ − 4x³ − 2x² + 12x +9 jest podzielny przez (x+1) 2. Aby nierówność była prawdziwa, to f(x) musi być podzielne przez (x+1)² 3. Hornerem dzielimy ... i co nam powstaje

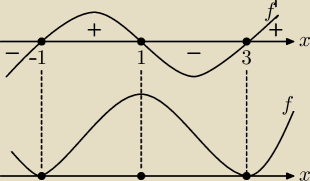
nieLaik: albo: f(x) = x⁴ − 4x³ − 2x² + 12x + 9 dla x∊ℛ f'(x) = 4x³ − 12x² − 4x + 12 = 4(x + 1)(x − 1)(x − 3) Funkcja f(x) osiąga minimum dla x = −1, maksimum dla x = 1, minimum dla x = 3 f(−1) = 1+4−2−12+9=0, f(1) = 1−4−2+12+9=16 > 0, f(3) = 81−108−18+36+9=0 zatem dla x∊ℛ f(x) ≥ 0