Optymalizacja - stożek i kula Kamil: W kule o promieniu R wpisano stożek, którego przekrój osiowy jest trójkątem równobocznym. Kule i stożek przecieto płaszczyzną równoległą do podstawy stożka, w odległości X od jego wierzchołka. Na płaszczyźnie tej utworzył się w ten sposób pierścień kołowy, którego okrąg zewnętrzny leży na powierzchni kuli, a okrąg wewnętrzny na powierzchni stożka. Dla jakiej wartości X pole tego pierścienia jest największe.

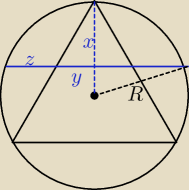
wredulus_pospolitus: P_pierścienia = π(z+y)² − πy² = πz(z+2y) z małego trójkąta prostokątnego (ekierkowego)

	√3
y =		x
	3

z Pitagorasa: z+y = √R² − (R−x)² = √2Rx − x² Nie będzie to ładne ... ale można doprowadzić wzór pola do postaci gdzie jedyną zmienną będzie 'x'

wredulus_pospolitus: Trzeba też zrobić drugi rysunek gdy x > R

wredulus_pospolitus: Albo szybko pokazać dlaczego na pewno x ≤ R

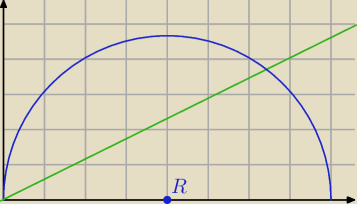
wredulus_pospolitus: alternatywnie: f(x) = √R² − (x−R)²

	√3
g(x) =		x
	3

P_pierścienia(x) = h(x) = π( f²(x) − g²(x) ) ; x∊(0;R)