Przekrój ostrosłupa Alaias: Przekrój ostrosłupa prawidłowego trójkątnego płaszczyzną zawierającą krawędź podstawy i środek jego wysokości ma pole równe 2√6. płaszczyzna przekroju jest nachylona do podstawy pod kątem 45^o. oblicz objętość tego ostrosłupa.

as:

	16
V=
	3

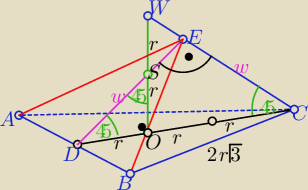
as: r −dł. promienia okregu wpisanego w podstawę ABC |DC|=h_p=3r |AB|=2r√3 P_p= 3r²√3 i H=|OW|=2r

	1
to V=		Pp*H
	3

V= 2r³√3 =======

	1
PABE=2√6 ⇒		*2r√3*w=2√6 ⇒ r*w=2√2
	2

W ΔDCE (równoramiennym i prostokątnym)

	3r√2
w=
	2

	3r2√2		2
zatem		=2√2 ⇒ 3r2=4 to r=
	2		√3

	8
V= 2*		*√3
	3√3

	16
V=
	3