wklęsłości i wypukłości essa: wyznacz przedziały wklęsłości i wypukłości oraz punkty przegięcia funkcji f(x)=1/lnx proszę o pomoc co bym nie robił nie wiem jak rozwiązać druga pochodna z góry dziękuję

wredulus_pospolitus: to policz jaka pochodne masz (pierwszą i drugą)

essa: policzyłem pierwszą wynik to f(x)= − 1/xlnx² ale problem jest z druga, nawet chat gtp podaje dwa wyniki...

wredulus_pospolitus: nie lnx² tylko ln²x <−−−− tak zapisujemy (lnx)² nie pytaj się chatgpt bo rozwiązania średnio poprawne podaje.

	1		1		1
f' = −		= −		*
	x(lnx)2		x		(lnx)2

	1		1		1		2		1
f'' =		*		+		*		*		=
	x2		(lnx)2		x		(lnx)3		x

	1		2
=		*(1 +		)
	(xlnx)2		lnx

korzystaj z WŁAŚCIWYCH narzędzi jak już szukasz pomocy: https://www.wolframalpha.com/input?i=%281%2F%28lnx%29%29%27%27 (taka uwaga −−− wolfram to 'hamerykański' produkt, więc log(x) oznacza tyle co nasz lnx)

essa: Okej, dzięki bardzo

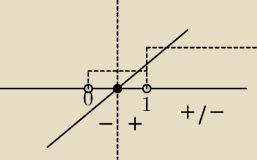
essa: być może ktoś mi pomoże i wytłumaczy, po podstawieniu do 0 wyniku drugiej pochodnej wychodzi x=1/e² dziedzina funkcji to (0,1)u(1,∞) ,wiec dlaczego f(x)>0 (wklęsła) jest tylko dla x ∊ (1/e² ,1) a wypukła >0 dla x ∊ (0, 1/e²) u (1,∞) skoro w przedziale od 1 do ∞ jest ponad wykresem?

wredulus_pospolitus:

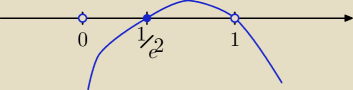
	1		2		1		lnx + 2
f'' =		*(1 +		) =		*
	x2ln2x		lnx		x2ln2x		lnx

	1
dla dowolnego x∊Df''		> 0 więc można go pominąć przy dalszych rozważaniach
	x2ln2x

(nie wpływa na znak f'') 1. O ile przy wyznaczaniu punktów przegięcia WYSTARCZY spojrzeć na licznik (kiedy licznik = 0) 2. O tyle przy sprawdzaniu kiedy f'' > 0 a kiedy f'' < 0 także MIANOWNIK ma wpływ na znak

lnx + 2		1
	> 0 ⇔ (lnx + 2)*lnx > 0 ⇔ x =		∨ x = 1
lnx		e2

wredulus_pospolitus: ojjj ... na odwrót wykres ale to już samemu poprawiasz

wredulus_pospolitus: popatrz ... że jak masz postać ułamkową potęgi to przy wyznaczaniu ekstremum lokalnego patrzysz tylko kiedy licznik = 0 ... ale do badania monotoniczności patrzysz na CAŁE WYRAŻENIE (chyba że mianownik jest > 0 dla dowolnego x∊D_f') tutaj dokładnie tak samo robisz.

essa: w jakim sensie wykres na odwrót? tak jak jest teraz pasuje...

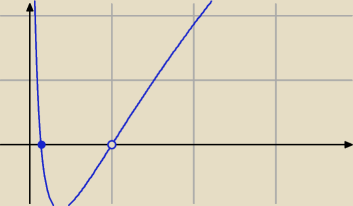
wredulus_pospolitus: g(x) = (lnx + 2)*lnx

wredulus_pospolitus: Pamiętasz zasadę rysowania szkicu wykresy funkcji metodą 'wężyka' Dlatego mówiłem 'na odwrót wykres'.

essa: wybacz ale dalej nie rozumiem, przy takim wykresie x ∊ (1,∞) powinno być wklęsłe ∪ bo leży nad wykresem czyli + a w odp jest ∩?

wredulus_pospolitus: sprawdź sobie na spokojnie co to jest wklęsłość a co to jest wypukłość. wykres który narysowałem odpowiada odpowiedzi: f(x) wypukła dla x ∊ (0, 1/e²) u (1,∞) (ponieważ f'' > 0 w tym przedziale) https://pl.wikipedia.org/wiki/Wypuk%C5%82o%C5%9B%C4%87_funkcji

essa: okej, mój profesor stosuje odwrotną terminologię dzięki jestem zobowiązany

wredulus_pospolitus: https://matematykadlastudenta.pl/strona/259.html jak 'odwrotną terminologię' Sprawdź na spokojnie notatki (innych studentów) i przede wszystkim książki które podał na pierwszych zajęciach.

essa: u mojego profesora f(x)>0 to funkcja wklęsła... człowiek starej daty być może dlatego w każdym razie już rozumiem dziękuje

ABC: w latach około 1980 w bloku wschodnim wypukła była "dupą do góry"

wredulus_pospolitus: @ABC ... tak ... ale to nadal było wypukła w górę i wypukła w dół ... a nie zamieniona wklęsłość i wypukłość ze sobą.