Tożsamość
#k:
Sprawdzic tożsamośc
| | 2a+√a2−b2 | |
b√2 |
| =√(a+b)3−√(a−b)3 |
| | √a+√a2−b2 | |
17 lis 01:24
#k:
Zapomniałem o załozeniu
a>b>0
17 lis 01:40
#k:
Mam pytanie .
Jak rozpisac prawą strone tej tożsamości aby skorzystać ze wzoru
A3−B3=(A−B)(A2+AB+B2)?
Dziękuje
17 lis 10:56
b: √(a+b)3 = (√a+b)3
Twoim A będzie √a+b
17 lis 12:20
#k:
Bardzo dziękuje za odpowiedz
17 lis 12:37
#k:
Wtedy prawa strona tak jak rozpisał b
(p{a+b)3−(p{a−b)3=(√a+b−√a−b)[(√a+b)2+√a+b*√a−b+(√a−b)2]=
=a+b+√a2−b2+a−b=2a+√a2−b2
Proszę o sprawdzenie czy jest dobrze
17 lis 20:07
#k:
Oczywiście ze zle bo nie wymnozylem drugiego nawiasu
17 lis 20:08
Mila:
Dobrze ta lewa strona przepisana?
17 lis 21:29
#k:
Dobry wieczór
Milu 
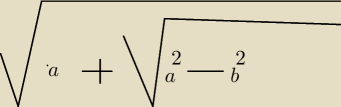
Dobrze jest przepisane .Mianownik tak jak na rysunku
17 lis 21:44
wredulus_pospolitus:
w liczniku masz 2a +
√a2−b2 
17 lis 21:49
#k:
Tak .
17 lis 21:55
b: | | 2a + √a2 −b2 | |
L = √2b |
| = |
| | √a + √a2 − b2 | |
| | 2a + √a2 − b2 | |
2b |
| = |
| | √a + b + 2√a2 −b2 + a − b | |
| | 2a + √a2 − b2 | |
2b |
| = |
| | √a+b + √a−b | |
| | (2a + √a2 − b2)(√a+b − √a−b) | |
2b |
| = P |
| | 2b | |
W poście z 20:07 po przejściu do nowej linijki został zgubiony czynnik A−B.
17 lis 22:33
#k:
Dziękuje Ci.
sam mianownik wiem jak przekształcic bo to pierwiastek surdyczny
17 lis 23:08
Mila:
Dzięki za wpis 21: 44.
Nie pisałam, bo już wpisał b, czy już się uporałeś z tym przykładem?
18 lis 15:26
#k:
Tak
Milu
Miałem problem z prawą stroną .
18 lis 18:53