Przebieg funkcji #k: Zadanie nr 9 Zbadaj przebieg zmienności funkcji f(x)=x²−|4x−4| x∊R a) sporządz wykres funkcji f podaj przedziały monotoniczności i ekstrema tej funkcji b) Odczytaj z wykresu liczbe rozwiązań równania x²−|4x−4|=mx w zależności od parametru m∊R

#k: Postaram sie potem zrobic to zadane do sprawdzenia

#k: 1)D_f=ℛ 2)Miejsca zerowe i współrzędne wierzchołka parabol Dla x∊(−∞,1] f(x)= x²+4x−4 x²+4x−4=0 Δ=32 √32=4√2

	−4−4√2
x1=		=−2−2√2
	2

x₂= −2+2√2

	−4
xw=		=−2
	2

	−32
yw=		=−8
	4

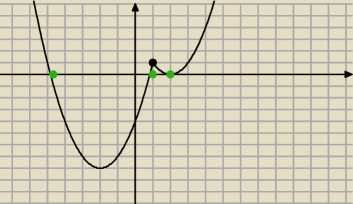
Dla x∊(1,∞) f(x)=x²−4x+4=(x−2)² (x−2)²=0 x₃=2 x_w=2 y_w=0 3) Dla x=1 funkcja nie jest różniczkowalna 4) wykres 5) Monotoniczność Funkcja maleje w przedziałach (−∞,−2) i (1,2) Funkcja rośnie w przedziałach (−2,1) i (2,∞) 6) Ekstrema f_min=f(−2)=−8 f_min=f(2)=0 f_max=f(1)=1 b) Dla : m∊(−∞,−8) równanie nie ma rozwiązań m=−8 równanie ma jedno rozwiązanie m∊(−8,0) równanie ma dwa rozwiązania m=0 rownanie ma trzy rozwiązania m∊(0,1) równanie ma cztery rozwiązania m=1 równanie ma trzy rozwiązania m∊(1,∞) równanie ma dwa rozwiązania prosze sprawdzić

wredulus_pospolitus: (b) NA PEWNO masz x²−|4x−4|=mx Bo jeżeli tak, to nie rozwiązałeś tego równania

#k: Tak. Taj jest w treści zadania

Mila: Równanie ma dwa rozwiązania dla m≤−8 lewą gałąź też przecina. Popatrz jeszcze i coś narysuj. x²−|4x−4|=−8x x≥1 x²−4x+4+8x=0 x²+4x+4=0 x=−2⊄D_r x<1 x²+4x−4+8x=0 x²+12x−4=0 Δ=160

	−12+4√10
x=		=−6+2√10<1 lub x=−6−2√10<1
	2

#k: Dziękuje