Kąt dwuścienny, uzasadnienie czworościanu foremnego K: Cosinus kąta zawartego między ścianami bocznymi ostrosłupa prawidłowego trójkątnego jest równy 1/3. Uzasadnij, że jest to czworościan foremny.

Tadeusz: zrób porządny rysunek to wszystko się wyjaśni

Tadeusz: ... no tak ... lepiej poczekać na "gotowca"

uszsz: Można też na Bizona

Tadeusz:

K: Nic rysunek nie dał, z tw. cos wychodzi mi równanie sprzeczne a² = 10a²/6. Umiem opisać wysokość trójkąta równoramiennego, który powstaje na boku, ale dalej nie wiem jak robić, bo żadne z krawędzi bocznych nie są podane.

aa:

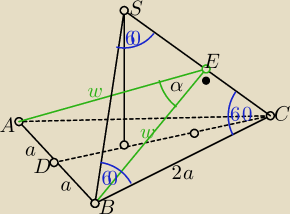
	w2+w2−4a2		1
cosα=		=		⇒ w=a√3
	2w*w		3

to ΔBCE jest trójkątem "ekierkowym" o kątach ostrych 30^o,60^o zatem ΔBCS jest równoboczy co kończy dowód Ostrosłup jest czwosościanem foremnym