geometria młodziutki: Dany jest okrąg o środku O. Wyznacz taki trójkąt równoboczny ABC, aby punkty A i B leżały na danym okręgu oraz aby odcinek OC miał możliwie największą długość. Ze zbioru pompe

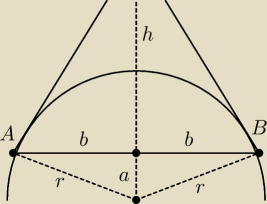
wredulus_pospolitus: mam dany TYLKO okrąg

	2b√3
|OC| = h + a =		+ √r2 − b2 = f(b) , b ∊ (0;r]
	2

Szukasz maksimum funkcji f(b) (gdzie 'r' to parametr)