Pierwiastki wielomianu zespolonego Kacper: Wyznaczyć liczbę z ∊ C wiedząc, że dwa kolejne pierwiastki pewnego stopnia z tej liczby wynoszą: z_k = 1+i z_k+1 = −1+i Mógłby ktoś proszę wytłumaczyć jak zabrać się do tego zadania?

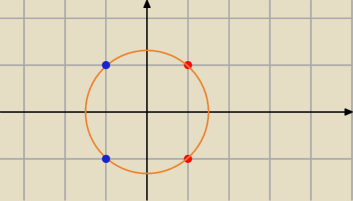
wredulus_pospolitus: 1. Zaznaczymy na płaszczyźnie pierwiastki. 2. Wiemy, że są to KOLEJNE pierwiastki. 3. Stąd mamy 'odległość' pomiędzy pierwiastkami ... i stąd mamy dwa kolejne pierwiastki ... stąd mamy wszystkie pierwiastki Czy znając wszystkie pierwiastki, jesteś w stanie wyznaczyć liczbę z

Kacper: Dziękuję. Czyli pierwiastki wielomianu zawsze tworzą okrąg na płaszczyźnie zespolonej?

ABC: Pierwiastki z liczby zespolonej tworzą okrąg , pierwiastki wielomianu nie muszą

Kacper: Rozumiem, dzięki wielkie za pomoc

wredulus_pospolitus: 'tworzą okrąg' −−− nie ... natomiast 'leżą na tym samym okręgu o środku w (0,0)' i co więcej −−− 'występują' one co ten sam kąt (w tym przypadku jest to 90^o)

Kacper: Jeśli kąt między dwoma kolejnymi pierwiastkami to α to znaczy to, że ilość wszystkich pierwiastków to będzie:

2π
	, tak?
α

ABC: Tak.