Prawdopodobieństwo Marta: Hej, nie mam pomysłu jak ugryźć to zadanie. Proszę o wyjaśnienie. Pewien zawodnik strzelający z pistoletu przy pierwszym strzale trafia do celu z prawdopodobieństwem 0,8. Zawodnik oddaje kolejno trzy strzały. W przypadku w poprzednim strzale trafił do celu, to prawdopodobieństwo trafienia w następnym strzale wzrasta o 0,05, a w przypadku, gdy nie trafi – maleje o 0,1. Oblicz prawdopodobieństwo tego, że zawodnik oddając trzy strzały dwukrotnie trafi do celu.

Aruseq: Rozrysuj sobie drzewko

wredulus_pospolitus: Bez rysowania drzewka: musimy rozpatrzeć takie możliwości: Trafił, trafił, nie trafił trafił, nie trafił, trafił nie trafił, trafił, trafił P(A) = 0.8*0.85*(1−0.9) + 0.8*(1−0.85)*0.75 + (1−0.8)*0.7*0.75 = 0.263

Marta: A dlaczego * 1−0.9 a nie 0,85−0,1 Dlaczego nie tak? P(A)= 0.8*0.85*0.75+0.8*0.7*0.75+0.7*0.75*0.8 Skąd bierze się to 1−0.9 1−0.85 i 1−0.8?

Marta: Chwila dobrze rozumiem, że to są po prostu zdarzenia przeciwne? trafił byłoby 0,8+0,1 czyli 0,9, a przeciwne 1−0,9?

wredulus_pospolitus: 1−0.9 <−−− prawdopodobieństwo nie trafienia gdy wcześniej dwukrotnie trafił analogicznie pozostałe Zapisałem w ten sposób, bo myślałem że łatwiej Ci będzie załapać niż gdybym pisał (odpowiednio) 0.1 , 0.15 , 0.2

Marta: Tak, to, że to jest prawdopodobieństwo nie trafienia to wiem. Tylko chciałam się upewnić, że ten zapis to inaczej zdarzenie przeciwne do trafienia. Zmyliło mnie to, że w treści jest napisane, że w przypadku nietrafienia prawdopodobieństwo maleje o 0,1. Czy jest jakiś sposób na to zadanie, w którym wykorzystujemy tą informację? Z Twojego rozwiązania wynika, że to jest niepotrzebna informacja, tak? Czy takie zadanie może pojawić się na maturze podstawowej?

Aruseq: wredulus wykorzystał tę informację. Weźmy przypadek: trafił, trafił, nie trafił. Przy pierwszym rzucie szansa na trafienie wynosi 0,8 − zgodnie z poleceniem. W drugim rzucie szansa na trafienie wynosi 0,85, gdyż wzrosła o 0,05, co wynika w trafienia poprzedniego rzutu. W trzecim rzucie szansa na trafienie ponownie wzrasta o 0,05, czyli wynosi obecnie 0,9. Chcemy jednak, aby zawodnik w tym rzucie nie trafił, wobec czego skoro szansa na trafienie wynosi 0,9, to szansa na nietrafienie to 1−0,9=0,1. Podobnie można przeanalizować pozostałe trzy przypadki. Patrząc na poziom zadań maturalnych − raczej mała szansa.

Marta: No właśnie, czyli to jest zdarzenie przeciwne, 1−0,9, to rozumiem. Tylko że w treści jest, że maleje o 0,1, czyli jak w pierwszym trafionym rzucie jest 0,8, to w drugim nietrafionym nie powinno być 0,8−0,1=0,7?

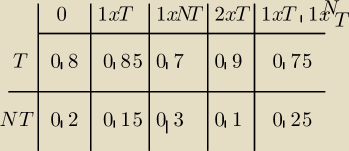
wredulus_pospolitus: Powyższa tabelka prezentuje jakie były prawdopodobieństwa trafienia (T) lub nietrafienia (NT). Gdy wcześniej mieliśmy: a) 0 −−−− brak strzałów (sytuacja startowa) b) 1x T −−− oddany 1 strzał, który był trafiony c) 1x NT −−− oddany 1 strzał, który był nietrafiony d) 2x T −−− oddane 2 strzały, oba trafione e) 1x T , 1x NT −−− oddane 2 strzały, jeden trafiony a jeden nietrafiony zauważ, że jak strzelamy ... mamy tylko dwie możliwości: trafimy w celu lub nie. Więc za każdym razem prawdopodobieństwo trafienia + prawdopodobieństwo spudłowania będzie równe 1 Informacja o tym, że prawdopodobieństwo trafienia wzrasta o 0.05 lub spada o 0.1 dotyczy jakie będzie 'nowe' prawdopodobieństwo w następnym strzale. Wyobraź sobie to w ten sposób: Jesteś na turnieju i to Ty strzelasz do celu. Gdy jesteś lekko poddenerwowana, trafiasz w 80% przypadku (prawdopodobieństwo trafienia wynosi 0.8). Jednak jesteś na turnieju, więc czujesz się poddenerwowana (w końcu chcesz wypaść jak najlepiej). I z każdym oddanym TRAFIONYM strzałem czujesz się bardziej pewnie/bardziej zrelaksowana (więc Twoja szansa na to że w kolejnych strzałach trafisz wzrasta). Natomiast z każdym kolejnym pudłem czujesz się bardziej poddenerwowana (więc Twoja szansa na to że w kolejnych kolejnych strzałach trafisz maleje) To co Ty proponujesz nie ma się nijak do tego co treść zadania mówi. 0.8 −−−− prawdopodobieństwo trafienia w pierwszym strzale 0.1 −−− o ile spadnie prawdopodobieństwo trafienia, jeżeli przed chwilą spudłowałaś 0.8 − 0.1 = 0.7 to nie będzie prawdopodobieństwo nietrafienia w drugim strzale To będzie prawdopodobieństwo trafienia w drugim strzale, w momencie gdy w pierwszym nietrafiłaś.

: ciekawe czy Robin Hood też tak szacował