nierownosci z wartoscia bezwzgledna barcik14: zadanie: |3/(x+1)|≥1 moja próba rozwiązania: −zakładam że x+1≠0, x≠−1 −tworzę 2 przypadki I) 3/(x+1)≥1 3≥x+1 2≥x II)3/(x+1)≤−1 3≤−x−1 4≤−x −4≥x − wynik: x∈(−∞;−4) wynik prawidłowy z odpowiedzi: x∈⟨−4;−1)U(−1;2⟩ czy ktoś mógłby wskazać mój błąd?

mm: Nierówność mnożymy obustronnie przez kwadrat mianownika!

3		3
	≥ 1 /*(x+1)2>0 lub		≤ −1 / * (x+1)2>0
x+1		x+1

teraz dokończ

barcik14: tym razem wyszło mi, że x∈(−∞;−4)U(2;∞), dalej nie pasuje to do odpowiedzi

mm: x≠ −1 3(x+1)≥(x+1)² lub 3(x+1)≤ −(x+1)² (x+1)(3−x−1)≥0 lub (x+1)(3+x+1)≤0 ( x+1)((2−x)≥0 lub (x+1)(x+4)≤0 x∊ (−1,2] lub x∊[−4,−1) Odp: x∊[−4,−1)U(−1,2] i pasuje

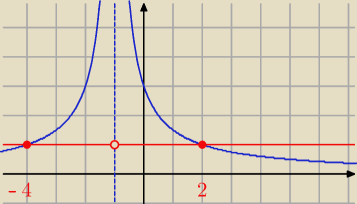
wredulus_pospolitus: Przecież dobrze Ci wyszło

wredulus_pospolitus: ach ... teraz widzę, że podałeś prawidłową odpowiedź a Twoje rozwiązanie do tego nie prowadzi Błędy masz 2. 1. Nie piszesz dla jakiego 'x' rozpatrujesz dany przypadek: I przypadek dla x> −1 (co daje rozwiązanie z przypadku −1 < x ≤ 2) II dla x < −1 2. w II przypadku gdy mnożysz obustronnie przez (x+1) nie zwróciłeś uwagi na to ... że (x+1) < 0 i w konsekwencji powinieneś zamienić znak nierówności wtedy z tego przypadku wyjdzie x ≥ −4 .... a po wzięciu części wspólnej z warunkiem przypadku (x<−1) masz −4 ≤ x < −1 dla tegoż przypadku

Stef:

3
	≥ 1 /* |x + 1| dla x ≠ −1 (wystarczy przemnożyć przez |x + 1|, a nie przez
|x + 1|

kwadrat mianownika) otrzymujemy: |x + 1| ≤ 3 ⇒ −3 ≤ x + 1 ≤ 3 ⇒ −4 ≤ x ≤ 2, uwzględniamy x ≠ −1, ostatecznie x ∊ <−4, −1)∪(−1, 2>

Iszo Song: tak tutaj masz racje bo |x+1| dla x≠−1 jest zawsze dodatnia