Kąty w trójkącie zbytniosiemartwisz: W trójkącie ABC punkt D jest środkiem odcinka AB. Kąt BAC ma miarę 40 stopni, a kąt CBA ma miarę 20 stopni. Oblicz miarę kąta ACD.

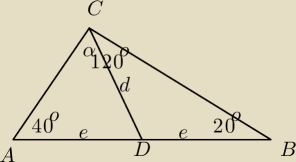
an: układ dwu równań z tw. sinusów i otrzymujemy

	cos20o
tgα=√3
	1−cos20o

α≈87,88^o

Jolanta: A może coś więcej ?

zbytniosiemartwisz: Czy mógłbym poprosić o rozpisanie tych równań?

an:

d		e
	=
sin20		sin(120−α)

d		e
	=
sin40		sinα

Jolanta: Gdy się umie to wszystko wydaje się jasne Ale jeżeli pyta się na forum o rozwiązanie tzn z się nie umie

zbytniosiemartwisz : Jolanta dobrze to ujęła Dziękuję za pomoc, z tymi równaniami już sobie poradziłem. Pozdrawiam

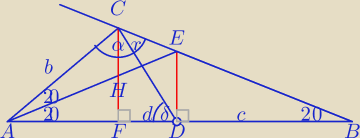
Mila: 1) AE− dwusieczna kąta A |AE|=|BE|, |AD|=DB|=c

|CE|		b
	=
|EB|		2c

========== 2) ΔAEC∼ΔABC 3) W ΔAFC: H=bsin(40^o) 4) W ΔCFB: Tales

|CE|		|EB|		|CE		d		d		b
	=		⇔		=		⇔		=		⇔
d		c		|EB|		c		c		2c

	b
d=
	2

====== 5) W Δ CFD: δ=x+20

	H		2bsin(40o)
tg(x+20)=		=
	b/2		b

tg(x+20^o)=2sin(40^o) dalej z tablic trzeba próbować; ==========