Nierówność Halinka: Zbiór (−2,∞) jest zbiorem rozwiązań nierówności (x−b)x²−3x−10)≥0. Wyznacz b Prosze o podpowiedz

wredulus_pospolitus: nie miało to być: (x−b)(x²−3x−10)

Halinka: Tak miało być

Halinka: Czy te nawiasy należy wymnożyc?

wredulus_pospolitus: Poza tym −− czy nie miało być [2,+∞)

wredulus_pospolitus: nie ... absolutnie nie wymnażaj tych nawiasów.

Halinka: Tak jest tam przedział zamknięty

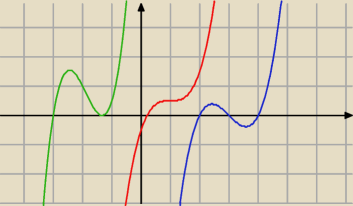
wredulus_pospolitus: 1. Zauważ, że W(x) = (x−b)(x²−3x−10) będzie wielomianem 3 STOPNIA, czyli będzie wyglądał jak jeden z rysunku powyżej 2. W zależności od tego jak wygląda wykres funkcji f(x) = W(x), będziemy mieli 1,2 lub 3 miejsca zerowe. 3. z tego jak jest zapisane możemy wyliczyć: x²−3x−10 = (x+2)(x−5) <−−− więc mamy 2 miejsca zerowe funkcji. 4. Jeżeli byłyby trzy miejsca zerowe (niebieska funkcja) to rozwiązaniem nierówności byłaby suma dwóch przedziałów (w przypadku niebieskiej funkcji byłoby to [2,3] u [4. +∞) ), a nie to mamy podane w treści zadania. Związku z tym musimy mieć tylko dwa miejsca zerowe (zielona funkcja). 5. W jaki sposób możemy to osiągnąć? Mając podwójny pierwiastek czyli gdy f(x) = (x−a)²*(x−c) ciąg dalszy nastąpi

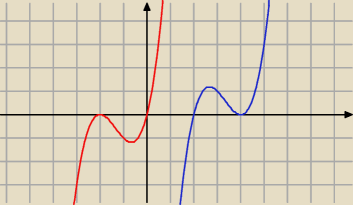
wredulus_pospolitus: Wcześniej wyjaśniłem Ci tok rozumowania z którego wynika dlaczego chcemy DOKŁADNIE dwa miejsca zerowe i jak by musiała wyglądać ogólna postać funkcji. 6. Stąd wiemy, (jak również z tego że x² − 3x − 10 = (x+2)(x−5) ) że (x−b) musi się równać ALBO (x+2) ALBO (x−5) −−− tylko to nam zagwarantuje dokładnie dwa miejsca zerowne. 7. ALE TO NIE KONIEC. 8. Spójrz na te dwie funkcje. Jak widzisz oba mają dwa miejsca zerowe, ale o ile w przypadku niebieskiej funkcji nierówność f(x) ≥ 0 będzie miała rozwiązanie [2 , +∞] o tyle w przypadku czerwonej funkcji będzie to {−2} u [0 , +∞) Tak więc ... chcemy, aby nasza funkcja wyglądała tak jak niebieska funkcja. 9. I teraz −−− pytanie brzmi −−− czy znamy metodę 'wężyka' wykorzystywanej do szkicowania funkcji wielomianowych przy obliczaniu nierówności

Halinka: Niestety nie było na zajęciach

wredulus_pospolitus: zapoznaj się z: https://matematykaszkolna.pl/strona/142.html

wredulus_pospolitus: możliwe, że nie miałaś podane nazwy (w sumie nazwa zapewne potoczna ). W każdym razie −−− mając na uwadze tą metodę możemy zrozumieć, że x₀ = 5 (a nie x₀ = −2) MUSI być tymże 'podwójnym' miejscem zerowym, bo wtedy dostaniemy analogiczny wykres do niebieskiego wykresu, co z kolei odpowiada temu jak ma wyglądać rozwiązanie f(x) ≥ 0