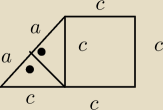
twierdzenie Pitagorasa krokodyl: dlaczego z tego nie wychodzi twierdzenie Pitagorasa

1		1		1
	*3c2=		a*b+		a*b+c2
2		2		2

Proszę nie podawać dowodu

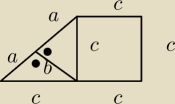
krokodyl: poprawiony rysunek

krokodyl: już wiem wynika to z własności kwadratu tam jest a a nie b

chichi: z równości, którą zapisałeś, wynika iż: c² = 2ab, no ale a = b, więc c² = 2a², więc c = a√2. co się oczywiście zgadza, dowiodłeś ale dla trójkąta prostokątnego, równoramiennego

krokodyl: dziękuję

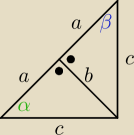
wredulus_pospolitus: Krokodyl ... wiem, że Ty się odnajdujesz się w swoim chaotyźmie ... ale My aż tak zdolni nie jesteśmy ... Tak trudno napisać skąd to równanie powstało Czemu musimy się domyślać 1. Sytuacja z rysunku ma prawo zajść w tylko jednej sytuacji, gdy α = β = 45^o −> czyli 2a = c√2 oraz a = b 2. A czemu miałoby wyjść tw. Pitagorasa

krokodyl: czy z tego wychodzi twierdzenie Pitagorasa bo mi nie wychodzi i nie wiem dlaczego?

krokodyl: nie potrafię wytłumaczyć dlaczego miało by to być twierdzenie Pitagorasa

krokodyl: to odpowiedź powyżej to do pytania wredulus_pospolitus

Mila: Krokodyl napisz pełną treść zadania, ponieważ nie potrafisz w sposób zrozumiały napisać jaki masz problem. Dowody twierdzenia Pitagorasa zobaczysz w książce "Śladami Pitagorasa"

krokodyl: chcę udowodnić twierdzenie Pitagorasa ale bez gotowych dowodów ja tutaj liczę tak że ten środkowy kwadrat i cztery trójkąty równają się temu dużemu prostokątowi i wychodzi mi c²=2ab a to chyba nie jest twierdzenie Pitagorasa

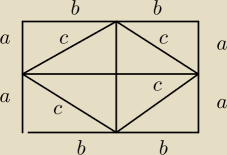
wredulus_pospolitus: pierwsza uwaga −−− środkowy 'kwadrat' nie jest kwadratem (jeżeli a≠b) tylko rombem.

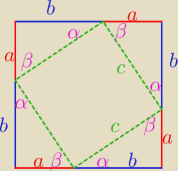
wredulus_pospolitus: tak budując kwadrat będziesz miał: P_{duzy kwadrat} = (a+b)² = 2ab + c² = P_{4x trójkąty} + P_{zielony kwadrat} a zielony jest kwadratem ponieważ α+β = 90^o

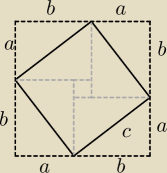
wredulus_pospolitus: Innnym podejściem będzie dorobienie linii w zielonym kwadracie i mamy:

	ab
c2 = 4*		+ (b−a)2 <−−− to ostatnie to pole tego malutkiego kwadraciku w środku
	2

Mila:

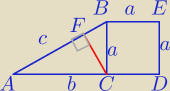
Mila: Linie pomocnicze. 1) Przyda się twierdzenie : (podobieństwo) W Δ prostokątnym kwadrat dł. przyprostokątnej jest równy iloczynowi dł. przeciwprostokątnej przez dł. rzutu prostokątnego tej przyprost. na przeciwprostokątną. Teraz działaj sam i wyjdzie wszystko jak należy.

krokodyl: Dziękuję