wredulus_pospolitus:
Możesz to wykazać poprzez indukcję matematyczną
w końcu wiemy, że (a+b)
n = (a+b)
n−1*(a+b)
Teraz zauważ jak powstaje kolejny wiersz w trójkącie Pascala
Pokombinujesz z tym
wredulus_pospolitus:
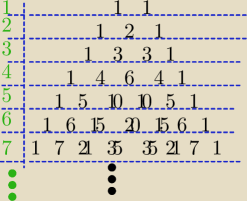
Wprowadźmy na moment oznaczenie dla wartości z trójkąta Pascala:
x
d,e, gdzie:
d −−−−
wiersz (innymi słowy − do jakiej potęgi podnosimy wyrażenie (a+b) )
e −−−−
który to jest element w trójkącie Pascala
Np. x
6,3 = x
6,5 = 15
Wiemy jak konstruowany jest kolejny wiersz trójkąta Pascala, mianowicie:
x
8,1 = x
7,1 = 1
x
8,2 = x
7,1 + x
7,2 = 1 + 7 = 8
x
8,3 = x
7,2 + x
7,3 = 7 + 21 = 28
x
8,4 = x
7,3 + x
7,4 = 21 + 35 = 56
....
x
8,8 = x
7,7 + x
7,8 = 7 + 1 = 8
x
8,9 = x
7,8 = 1
(na trójkącie lepiej to widać, ale mam nadzieję, że rozumiesz o co mi chodzi w tym zapisie)
Przyjrzyjmy się teraz co mają reprezentować liczby w trójkącie Pascala.
Dzięki trójkątowi Pascala mam możliwość wyszukania jakie wartości będą po wymnożeniu (a+b)
n,
np. (a+b)
5 = 1*a
5 + 5*a
4b
1 + 10*a
3b
2 + 10*a
2b
3 + 5*a
1b
4 + 1*b
5
Niezależnie od tego wiemy, że (a+b)
5 = (a+b)
4*(a+b)
Mając to za sobą możemy przejść do indukcji matematycznej.
Przeprowadzę ją dla KONKRETNEGO 'n' (n=4) −−− wydaje mi się, że widząc konkretne liczby łatwiej
Ci będzie 'załapać' ideę samego dowodu
Ty już sama po przeanalizowaniu tego powinnaś dać radę to zrobić dla 'n = k'.
To będzie kwestia przerobienia paru znaczków, skorzystania z tego oznaczenia symboli z
trójkącie: x
d,e, oraz skorzystania z faktu jak powstaje element x
d+1 , e <−−− o czym
pisałem powyżej.
(Pseudo) indukcja:
1. n = 1
(a+b)
1 = 1*a + 1*b −−− zgadza się
2. n = 4 (tu powinno być n = k)
(a+b)
4 = 1*a
4 + 4*a
3b
1 + 6*a
2b
2 + 4*a
1b
3 + 1*b
4
3. n = 4 + 1 (tu powinno być n = k+1)
(a+b)
5 = (a+b)
4*(a+b) = // korzystamy z (2) // =
= (1*a
4 + 4*a
3b
1 + 6*a
2b
2 + 4*a
1b
3 + 1*b
4)*(a+b) =
= 1*a
5 + 5*a
4b
1 + 10*a
3b
2 + 10*a
2b
3 + 5*a
1b
4 + 1*b
5
c.n.w. (gdyby to było dla n = k
)
PS. tak wiem ... obciąłem trójkąt Pascala, bo zaczyna o się od (a+b)
0 = 1 (ale nie chce mi
się już przerabiać rysunku, więc zostaje tak jak jest).
czy mozna prosić jaśniej?
