wzór Shen Li : Dobry wieczór Wyprowadz stosując tylko twierdzenie Pitagorasa wzór b_2n= √2−√4−b_n² gdzie b_n− bok wielokąta foremnego wpisanego w okrąg o promieniu 1 b_2n−bok 2n−kąta Dziękuję

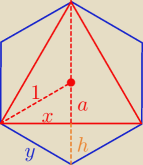
wredulus_pospolitus: Zakładam, że wielokąt o boku b_2n także jest wpisany w tenże okrąg. dla n = 2k+1 powyższy rysunek b_n = 2x h = 1 − a

	1
a = √1 − x2 =		√4 − bn2
	2

	1
h = 1 − a = 1 −		√4−bn2
	2

	bn2		4 − bn2
y2 = x2 + h2 =		+ 1 − √4−bn2 +		= 2 − √4−bn2
	4		4

y = √2 − √4−b_n² c.n.w.

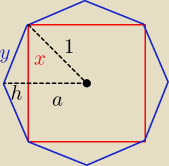
wredulus_pospolitus: dla n = 2k podaję sam rysunek ... masz dokładnie to samo podejście ... w sumie jak teraz to narysowałem ... to nawet nie trzeba było rozdzielać na przypadki

Shen Li : Dziekuje .

Mariusz: Czy bawisz się metodą Archimedesa obliczania przybliżonej wartości liczby π Twoje zadanie to podstawowy krok tej metody