sprawdź czy istnieje taki ostry kąt alfa dla ktorego sin alfa=(3√34)/34 i tg alf Alicja: sprawdź czy istnieje taki ostry kąt alfa dla ktorego sin alfa=(3√34)/34 i tg alfa=4/5 Wychodzą mi jakieś przeogromne kwoty, nie mam pojęcia gdzie jest haczyk

Alicja: wychodzą mi jakieś przeogromne kwoty, wiele zadań tego typu robiłam i było ok, nie mam pojęcia , bo chyba gdzies popelniam cały czas ten sam błąd

Mila:

	3√34
sinα		i tg α=4/5, α− kąt ostry
	34

usuwamy niewymierność z licznika:

	3
sinα=
	√34

	3
(		)2+cos2α=1
	√34

9
	+cos2α=1
34

	9
cos2α=1−
	34

	25		5
cos2α=		, cosα
	34		√34

	sinα		3		√34
tgα=		=		*
	cosα		√34		5

	3
tgα=
	5

========

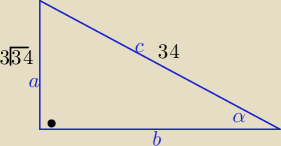
Eta: α−− kąt ostry

	a		3√34
sinα=		=
	c		34

b=√34²−9*34= 5√34

	a		3√34		3		4
tgα=		=		=		≠
	b		5√34		5		5

Odp: taki kąt α nie istnieje

Alicja: Mila, jesteś wielka. W I E L K A I S U U U U P E R Bardzo dziękuje, ale skąd pomysł na usunięcie niewymierności z licznika − z mianownika to kumam OK, ale z licznika?

#k: Niespodzianka Taka sama sytuacje będzie miała miejsce gdy bedzie np do policzenia z definicji pochodna z f(x)= √x w punkcie x₀=2

Alicja: Noo, niespodzianka i to jedyna taka ))) OK, super, rozumiem, mądrzy ludzie tu zaglądają, ale tak bez niespodzianki − jest w ogóle szansa na rozwiązanie tego zadania

Mila: Alicjo , usunęłam niewymierność z licznika z lenistwa. Nie chciałam podnosić 34 do kwadratu, wolałam √34, jak widzisz uprościło to rachunki. Nie zawsze należy się spieszyć z usuwaniem niewymierności z mianownika, wszystko zależy od tego co będziemy dalej robić z taką liczbą.

Mila: Ćwiczenie z niewymiernością. Wyznacz x: √5 x+2 x= 4

Alicja: cd (√5+2)x=4 /:(√5+2) x=4/(√5+2) usuwamy niewymierność z mianownika mnożąc licznik i mianownik przez (√5−2) w mianowniku wyjdzie nam 5−4 czyli jeden i ostatecznie x=4√5 ? Mila az się boję (

Aruseq: 4(√5−2)

Alicja: tak dokładnie )))) na koncu zawaliłam

getin:

	5√17		8√29
Przy wszelkich zadaniach wymagających podnoszenia liczb typu		albo		,
	17		29

że zawartość pierwiastka w liczniku jest taka sama co mianownik, zawsze warto robić to co zrobiła Mila

getin: *podnoszenia liczb do kwadratu

Alicja: Super dzięki

Mila: Alicjo, można prościej. (wg mnie) (√5+2)x=4 /*(√5−2) (5−4)*x=4*(√5−2) x=4*(√5−2) Obyło się bez usuwania niewymierności z mianownika.

Alicja: mozna

getin: Mila przedstawia sprytne sposoby na takie pierwiastki. Dzięki Nie znałem ich

chichi: może nie wymnażać po podniesieniu do potęgi, tylko po prostu skrócić i nie ma wielkich liczb

rosebl: Agario is an engaging online game where you control a cell, devouring smaller cells to grow and avoiding being devoured by larger players. https://agargame.io

Itzel: Czuję, że w zadaniu może kryć się błąd – czy na pewno wartości sinus i tangens dotyczą tego samego kąta? Jeśli nie, to może warto sprawdzić, czy nie doszło do pomyłki w oznaczeniach? https://incredibox-game.io/home

aivon: Thank you for such an amazing post. It was very informative and helpful. Keep going https://vidtext.ai/

Humanize AI: Tired of opening too many tabs to access different writing and research tool websites? We understand your frustration, so Humanize AI provides One−stop Writing Assistant Humanize AI: https://humanizeai.tools/humanize-ai

DeepseekTurkce: Ciekawe zadanie, Alicja! Rzeczywiście, warto sprawdzić, czy wartość sin(α) = (3√34)/34 rzeczywiście mieści się w przedziale dopuszczalnym dla sinusa kąta ostrego — a wygląda na to, że tak. Jeśli tg(α) = 4/5, to możesz też sprawdzić to przez zależność między tangensem i sinusem: sin(α) = tg(α) / √(1 + tg²(α)). Może pomoże Ci to złapać ten “haczyk”. A jeśli nadal coś nie gra, spróbuj wrzucić to do https://deepseekturkce.com/ − świetnie radzi sobie z takim typem problemów matematycznych krok po kroku.

snow: Join the ride with sled in snow rider 3d game https://snowrider-3dgame.github.io/

GPTDeutsch: Też kiedyś się nad tym głowiłam! Tutaj faktycznie wszystko wygląda na poprawne – skoro sin(α) = (3√34)/34, to warto sprawdzić, czy tg(α) = sin(α)/cos(α) rzeczywiście daje 4/5. Możliwe, że chodzi o uproszczenie pierwiastków albo błąd przy przekształcaniu cosinusa. Ja w podobnych sytuacjach wrzucam wzory do https://gptdeutsch.net/ – świetnie tłumaczy krok po kroku, gdzie może być haczyk. Polecam!

ChatGPTUkrainian: Miałem podobny problem, ale sprawdziłem to z https://xn--80ag0bkcz.net/ i wszystko się zgadza – jeśli sin α = (3√34)/34 i tg α = 3/5, to coś nie gra, bo tg α powinna wtedy wynosić 3/5, nie 4/5. Może warto jeszcze raz policzyć cos α?

adrianmichael: Sprawdzenie, czy istnieje taki ostry kąt α, dla którego sin ⁡ 𝛼 = 3 34 34 sinα= 34 3 34 ​ ​ i tan ⁡ 𝛼 = 4 5 tanα= 5 4 ​ , prowadzi do sprzeczności. Po obliczeniach, które przeprowadziłaś, wynika, że wartość tan ⁡ 𝛼 tanα nie zgadza się z wyliczonym sin ⁡ 𝛼 sinα. W związku z tym, taki kąt 𝛼 α nie istnieje. Odpowiedź: taki kąt 𝛼 α nie istnieje. https://meme-soundboard.net/

gptdeutsch: Willkommen bei GPTDeutsch.com das auf GPT−5, Ihrer führenden Plattform für ChatGPT im deutschsprachigen Raum. Erleben Sie die Revolution der Künstlichen Intelligenz, maßgeschneidert für Ihre Bedürfnisse – sofort nutzbar, ohne Registrierung und mit den neuesten OpenAI−Modellen. Sie können chatgpt kostenlos nutzen unter https://gptdeutsch.com/