promienie Magdaa_00: Dlaczego promień okręgu wpisanego w trapez równoramienny i promień okręgu opisanego na trapezie równoramiennym leży na jednej prostej?

Hua Zhi: Według mnie pytanie jest żle postawione . Powinno byc takie . Dlaczego środek okręgu wpisanego w trapez równoramienny i środek okręgu opisanego na trapezie równoramiennym leżą na jednej prostej Najpierw zrobiłbym rysunek takiego trapezu równoramiennego w który można wpisać okrąg i jednocześnie na którym można opisać okrąg i zobaczyłbym gdzie te środki leżą O ile prosto wytłumaczyc ze srodek okręgu opisanego leży na osi symetrii trapezu to nie bardzo wiem na teraz jak wytłumaczyc ze srodek okręgu wpisanego leży na tej samej osi

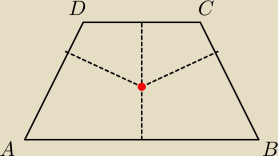
wredulus_pospolitus: Dokładnie w ten sam sposób −−− skoro mamy trapez równoramienny ... to odległość środka okręgu wpisanego w tenże trapez od ramion musi być taka sam (równa 'r') −−− związku z tym środek okręgu MUSI leżeć na osi symetrii tegoż trapezu. A odnośnie okręgu opisanego −−− podobna argumentacja − tylko patrzymy na analogicznego odległości do wierzchołków A i B lub D i C

Hua Zhi: Rozumiem . natomiast co do okręgu opisanego to tłumzczyłem sobie w ten sposób ze srodek takiego okregu lezy na przecięciu sie symetralnych boków a jedna z symetralnych jest os symetrii tego trapezu

wredulus_pospolitus: oczywiście −−− żeby dowód był dowodem − warto by było narysować trójkąty prostokątne i po prostu wykazać, że są one przystające − ale autorka pytała się 'dlaczego' a nie 'jak wykazać', więc nie chce mi się w to bawić.