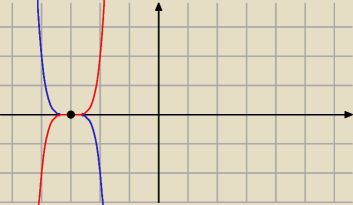
granice Z.K: f(x)=2(x+3)⁵ czerwony g(x)=−2(x+3)⁵ niebieski lim f(x)=∞ ⇔⋀ ⋁ ⋀ f(x)>A gdzie A to dowolna duża liczba x→∞ A x₀ x>x₀ więc według mnie będzie także lim f(x)=(−∞) ⇔ ⋀ ⋁ ⋀ f(x)>A x→∞ A x₀ x>x₀ jest do wykazania że lim(−2(x+3)⁵)=−∞ x→∞ g(x)>A A>0 −2(x+3)⁵>A

	1
(x+3)5<−		A
	2

	1
x+3<5√−		A
	2

	1
x+3<−		5√A
	2

	1
x<−		5√A−3
	2

	1
Liczby x<−		5√A−3 sa dostaecznie wielkie na to aby było g(x)>A
	2

Z.K: Wiem że sa narzędzia do badania granic funkcji w (−∞) i (∞) ale chciałbym to zrobic dla zasady

wredulus_pospolitus: To co podajesz to tw Cauchy'iego dotyczące granicy niewłaściwej ciągu. ∀_{A < 0 , A ∊ R} ∃_x0∊Df ∀_{x > xo , x∊Df} f(x) < A Wybieramy: A < 0

	A
Niech xo = (−		)1/5 − 3 (to tak naprawdę wypisujemy później ... gdy zobaczymy 'co
	2

potrzebujemy' f(x) = −2(x+3)⁵ < −2(x_o+3)⁵ = A

Z.K: tak mam wredulus podane w podreczniku do 2 klasy i jest rozwiązany przyklad

	1
W1(x)=		(x−1)3
	3

mamy uzasadnic ze przy x→∞ W1(x)→∞ Postąpiłem podobnie

wredulus_pospolitus: tyle że masz w złą stronę znak nierówności ... od samego początku

Z.K: https://zapodaj.net/plik-U6Vjc2dZvz https://zapodaj.net/plik-EDzEH8PrbG https://zapodaj.net/plik-mAY8kA3wGo https://zapodaj.net/plik-XgFYDBtnDD

Z.K: Zobacz na te skany i to jest zadanie nr 174

wredulus_pospolitus: ja się nie czepiam metody ... ja się czepiam: g(x)>A A>0 g(x) < A oraz A <0 bo chcesz granicę niewłaściwą (−∞) wykazać. zauważ, że wyszło Ci : x < −⁵√A/2 − 3 czyli TYLKO dla UJEMNYCH x'sów, A piszesz o "wystarczająco dużych x'sach" niby jak duże one są skoro są one mniejsze od 0

Z.K: Ok. Teraz dalej oglądam serial