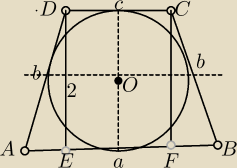
 Na kole o promieniu r=1cm opisano trapez równoramienny o polu S cm2.
Wyznacz długości podstaw trapezu jako funkcje S
Wyznacz dziedziny tych funkcji
Oblicz długości podstaw trapezu dla
1) S=3 2) S=4 3)S=5 4) S=16
Na kole o promieniu r=1cm opisano trapez równoramienny o polu S cm2.
Wyznacz długości podstaw trapezu jako funkcje S
Wyznacz dziedziny tych funkcji
Oblicz długości podstaw trapezu dla
1) S=3 2) S=4 3)S=5 4) S=16
| a+c | a+c | |||
S= | *h= | *2=a+c | ||
| 2 | 2 |
| a−c | ||
a=c+2*AE ale AE= | i mi tu cos nie pasuje | |
| 2 |
 a = c + 2*|AE| −−> a − c = 2*|AE| −−> |AE| =
a = c + 2*|AE| −−> a − c = 2*|AE| −−> |AE| = 
| a−c | ||
a=c+2*AE=c+2* | =c+a−c=a | |
| 2 |
 UWAGA
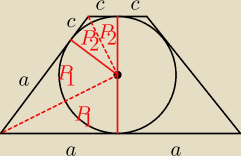
UWAGA  Wprowadzam odrobinkę inne oznaczenia (bo nie lubię ułamków).
Przy tych oznaczeniach:
|AE| = a − c
i teraz tw. Pitagorasa:
(a+c)2 = 22 + (a−c)2 −−−> 4ac = 4 −−−> ac = 1 −−> 2ac = 2
a korzystając z tego co policzone zostało przez Ciebie (i biorąc poprawkę na zmienione
oznaczenia):
S = 2(a+c) −−−> 2a = S − 2c
więc mamy: (S−2c)*c = 2 −−−> c =
Wprowadzam odrobinkę inne oznaczenia (bo nie lubię ułamków).
Przy tych oznaczeniach:
|AE| = a − c
i teraz tw. Pitagorasa:
(a+c)2 = 22 + (a−c)2 −−−> 4ac = 4 −−−> ac = 1 −−> 2ac = 2
a korzystając z tego co policzone zostało przez Ciebie (i biorąc poprawkę na zmienione
oznaczenia):
S = 2(a+c) −−−> 2a = S − 2c
więc mamy: (S−2c)*c = 2 −−−> c =  −−−> a =
−−−> a = 
 ? i 2a =
? i 2a = 
