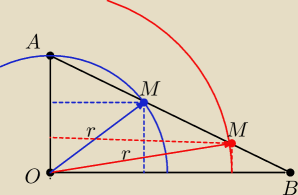
Trójkąt i okrąg Z.K: Dany jest trójkat AOB ∡AOB=90^o |AO|=2cm BO=4cm Kreślimy okrąg o środku O i promieniu r . Okrąg ten przecina przeciwprostokątną AB w punkcie M . Wyznacz odległości puntu M od przyprostokątnych AO i BO jako funkcje parametru r Wyznacz dziedziny tych funkcji , Oblicz te odległości dla r=1 r=1,5 r=3 r=5

	4
r=		√5 r=2 r=4
	5

Najwazniejsze to wyznaczyc te funkcje Rysunek zrobiłem sam

wredulus_pospolitus: Wprowadźmy układ współrzędnych. Niech punkt O ma współrzędne (0,0). Wtedy: M ma współrzędne (x , −x/2 + 2) ; x ∊ [0 ; 4] natomiast odległość punktu M od przyprostokątnych (czyli także osi OX i OY) wynoszą:

x
	+ 2 oraz x
2

z tw. Pitagorasa:

	x
r2 = x2 + (2 −		)2 −−−> (bo nie lubię ułamków) −−−> 4r2 = 4x2 + (4 − x)2
	2

Do tego samego można dojść wykorzystując podobieństwo trójkątów. 4r² = 4x² + (4 − x)² −−−> 5x² − 8x + 16 = 4r² −−−>

	4		16		16
−−−> 5(x2 − 2*1*		x +		) −		+ 16 = 4r2 −−−>
	5		25		5

	4		16
−−−> 5(x −		)2 = 4(r2 −		) −−−> (x − 4/5)2 = 4/5 * (r2 − 16/5) −−−>
	5		5

	4
−−−> x =		± √4/5 * (r2 − 16/5)
	5

	4
−−−> f(r) =		± √4/5 * (r2 − 16/5)
	5

	4   ± √4/5 * (r2 − 16/5) 5
−−−> g(r) = 2 −
	2

o ile gdzieś się nie walnąłem. Przy okazji: jeżeli r > MAX{|AO| , |BO|} −−−> brak punktu M. jeżeli r < h_Δ −−−> brak punktu M jeżeli r > 2 ∨ r = 4 −−−> jedna możliwa lokalizacja punktu M jeżeli r ∊ [2, 4) −−−> dwie możliwe lokalizacje punktu M

	|AO|*|BO|		8		2√5
hΔ =		=		=		≈ 0.89
	|AB|		√20		5

wredulus_pospolitus:

	√5
coś skopałem ... hΔ = 4
	5

i miało być −−−> r ∊ (h_Δ ; 2] −−−> dwie możliwe lokalizacje punktu M a dla r = h_Δ jedna lokalizacja Już nie myślę

Z.K: Wredulus juz jutro jak sie ogarne z rana popatrze na razie dzięki .Teraz dobranoc