Eksperyment losowy polega na wylosowaniu dwóch liczb z przedziału [−1, 1]. Zakła Tomek: Eksperyment losowy polega na wylosowaniu dwóch liczb z przedziału [−1, 1]. Zakładamy, że wylosowanie każdej liczby jest jednakowo prawdopodobne. Prawdopodobieństwo tego, że wartość bezwzględna sumy tych liczb będzie mniejsza od 1 jest równe: 1/4 Może ktoś potwierdzić?

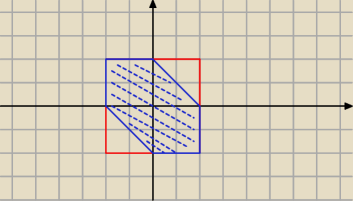
wredulus_pospolitus: Nie ... prawdopodobieństwo będzie ilorazem zakreskowanego pola do pola kwadratu o boku 2, Na chłopski rozum ... chcemy aby |x+y| < 1 −−−− zauważ, że jeżeli x < 0 ; y > 0 (albo na odwrót) to jest to spełnione ... więc już na wstępie masz P ≥ 1/2

wredulus_pospolitus: algebraiczne podejście: |x+y| < 1 −−−> 1. x+y > 0 ; y < −x + 1 2. x+y < 0 ; y > −x − 1 stąd masz te ograniczenia (oczywiście ... zawężone do Ω)

Tomek: Czyli 3/4 z tego wychodzi?

wredulus_pospolitus: Da