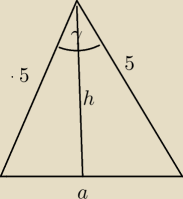
trójkat równoramienny Z.K: Ramie trójkata równoramiennego ma długośc 5 Oblicz długości wysokości i podstawy trójkata jesli dane jest pole S tego trójkata S=12

1
	a*h=12
2

	1
h2+		a2=25
	2

	1
h2=25−		a2
	4

	1
h=√25−		a2
	4

	1
25−		a2>0
	4

1
	a2<25
4

a²<100 a∊(0,10)

1		1
	a*√25−		a2=12
2		4

1		1
	a2(25−		a2)=144
4		4

25		1
	a2−		a4=144
4		16

100a²−a⁴−2304=0 −a⁴+100a²−2304=0 a⁴−100a²+2304=0 Δ=10000−9216=784 √784=28

	100−28
a12=		=36 a1=6 lub a1=−6 odpada
	2

	100+28
a22=		=64 a2=8 lub a2=−8 odpada
	2

	1
Dla a=6 h=√25−		*36=4
	4

	1
dla a=8 h=√25−		*64=3
	4

W sumie chciałem to robic z twierdzenia cosunusów ale w ksiązce były dwie odpowiedzi i z twierdzenia cosinusów nie wychodziły takie całkowite odpowiedzi

wredulus_pospolitus: Chciałeś skorzystać z cosα i cos(α/2) do tw. cosinusów To dobrze że tego nie uczyniłeś , ale można też było inaczej zrobić:

	52		24		√625 − 576		7
P = 12 =		*sinα −−−> sinα =		−−−> cosα = ±		= ±
	2		25		25		25

i teraz tw. cosinusów:

	7
1. a2 = 25 + 25 − 2*25*		= 50 − 14 = 36 −−−> a = 6 −−> h = 4
	25

	7
2. a2 = 25 + 25 + 2*25*		= 50 + 14 = 64 −−−> a = 8 −−−> h = 3
	25

wredulus_pospolitus: Jak już wcześniej pisałem −−−−− Ty chyba lubisz liczyć deltę

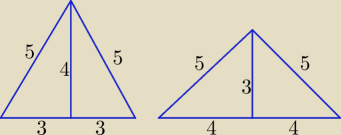aa: P=12

Z.K: Dziękuje za pomoc wredulus tak jakoś wychodzi z ta deltą

Z.K: Teraz tak patrze co napisałes o 21 : 57 to własnie tak liczyłem −tylko zamiast ułamki zwykłe dalem dziesiętne Przy zwykłych sie skraca .

wredulus_pospolitus: W zadaniach raczej nie zalecałbym używania zapisu dziesiętnego dla ułamków.