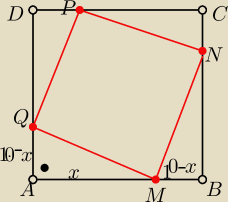
 W kwadrat ABCD o boku 10cm wpisano kwadrat MNPQ tak że wierzchołki MNPQ leżą odpowiednio na
bokach AB, BC,CD,DA.
POle kwadratu MNPQ stanowi
W kwadrat ABCD o boku 10cm wpisano kwadrat MNPQ tak że wierzchołki MNPQ leżą odpowiednio na
bokach AB, BC,CD,DA.
POle kwadratu MNPQ stanowi
| 3 | ||
1) | ||
| 4 |
| 1 | ||
2) | ||
| 2 |
| 1 | ||
3) | pola kwadratu ABCD . | |
| 5 |
| 1 | ||
PMNPQ=100−4* | x(10−x)= 100−2x(10−x)=100−20x+2x2=2x2−20x+100 | |
| 2 |
| 20−10√2 | 1 | |||
x1= | =5− | 5√2>0 | ||
| 4 | 2 |
| 1 | ||
10−x1=5+ | 5√2>0 | |
| 2 |
| 1 | ||
x2=5+ | 5√2>0 | |
| 2 |
| 1 | 1 | |||
10−x2=10−(5+ | 5√2)=5− | 5√2>0 | ||
| 2 | 2 |
| 1 | 1 | |||
Więc trójkąty sie utworzy wiec AM=5− | 5√2 lub AM=5+ | 5√2 | ||
| 2 | 2 |
 Fajnie, że wyciągnąłeś wniosek z poprzedniego zadania jak podejść do tego typu zadań.
Ale pokażę Ci coś jeszcze innego, z czego bym skorzystał tutaj:
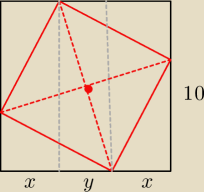
1. Środki kwadratów są w tym samym punkcie
2. d ∊ [ 10 , 10√2 ) (d − przekątna czerwonego kwadratu)
Fajnie, że wyciągnąłeś wniosek z poprzedniego zadania jak podejść do tego typu zadań.
Ale pokażę Ci coś jeszcze innego, z czego bym skorzystał tutaj:
1. Środki kwadratów są w tym samym punkcie
2. d ∊ [ 10 , 10√2 ) (d − przekątna czerwonego kwadratu)
| 1 | ||
P = d2 −−−> Pmin = dmin2 = 102 = 100 = | P stąd wiemy, że (c) | |
| 2 |
| 3 | ||
(a) d2 = | *200 = 150 −−> d = √150 −−−> | |
| 4 |
