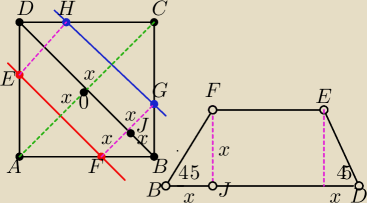
Kwadrat Z.K: W kwadracie o boku 12 cm poprowadzono dwie proste równoległe do przekatnej kwadratu w równych od niej odległościach . Proste podzieliły kwadrat na 3 części o równych polach . Oblicz odległości prostych od przekątnej kwadratu P_□=144cm² Pole jednej części wynosi P=48cm² = P{EAF}=48cm² P_DAB=72 cm² P_BDEF =P_DAB−P_EAF=24cm² Z trójkata prostokątnego FBG mamy że |FB|=|DE|=√2x Trapez BDEF jest trapezem równoramiennym o kącie przy podstawie BD równym 45^o W trapezie tym |BD|=12√2 |FE|=12√2−2x P_BDEF=24

12√2+12√2−2x
	*x=24
2

24√2−2x
	*x=24
2

(12√2−x)*x=24 12√2x−x²=24 −x²+12√2x−24=0 x²−12√2x+24=0 Δ=288−96=192 √192=8√3

	12√2−8√3
x1=		=6√2−4√3
	2

x₂=6√2+4√3 >od AO=6√2 więc to rozwiązanie odpada Odległośc prostej od przekątnej wynosi 6√2−4√3 Pewnie można prościej

wredulus_pospolitus: oczywiście że można.

	1
Skoro mamy 3 takie same pola, to .... znaczy że pole trójkąta =		P□
	3

Co więcej, wiemy że ten trójkąt jest trójkątem równoramiennym prostokątnym.

	x2		1
PΔ =		=		*122 −−−> x2 = 96 −−−> x = 4√6
	2		3

Stąd wysokość poprowadzona z wierzchołka A (pokrywająca się z przekątną kwadratu) =

	1
=		*4√6*√2 = 4√3
	2

	1
Połowa przekątnej kwadratu =		*12√2 = 6√2
	2

Stąd odległość prostych od drugiej przekątnej = 6√2 − 4√3

Z.K: Ok

wredulus_pospolitus: Ty chyba lubisz liczyć Δ