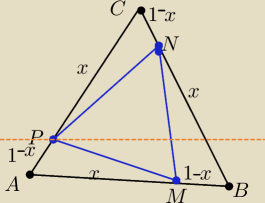
Pole trójkata MNP Z.K: Dany jest trójkat równoboczny ABC na bokach AB BC CA zaznacz odpowiednio punkty M N P tak że |AM|=|BN|=|CP|=x |AB|=1 dcm Zbadaj pole trójkata MNP jako funkcje x |AB|=|BC|=|CA|=1 |AM|=|BN|=|CP|=x |MB|=|NC|=|PA|=1−x ∡|CAB|=∡|ABC|=∡|BCA|=60^o |PM|=|MN|=NP| z przystawania bkb |PM|²=|PA|²*+|AM|²−2*|PA|*|AM|*cos60^o |PM|²=(1−x)²+x²−(1−x)*x=1−2x+x²+x²−x+x²=3x²−3x+1

	(3x2−3x+1)√3
PNMP=
	4

A jak to ewentualnie zrobic bez twierdzenia cosinusów?

wredulus_pospolitus:

	√3
PABC =
	4

	√3		x*(1−x)*sin60o
PNMP = PABC − 3*PAMP =		− 3*		= ...
	4		2

odrobinkę szybciej i mniejsza szansa na zrobienie błędu