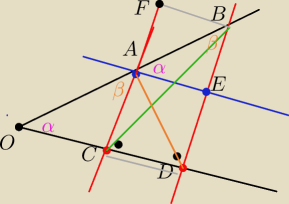
Cwiczenie Z.K: Udowonic twierdzenie Jeżeli dwie proste równoległe odcinaja na jednym z ramion kąta równe odcinki to równiez odcinki odcięte na drugim ramieniu sa równe |OA|=|AB| i AC||BD Mamy pokazac ze |OC|=|CD| Przez punkt A prowadzę prostą równoległa do prostej OD Przetnie ona prosta BD w punkcie E ΔOAC≡ΔAEB na podstawie cech kbk mamy stąd |OC|=|AE| Równiez |AE|=|CD| Stąd |OC|=CD| Następnie jest cwiczenie 24. Określ odlegoś dwóch prostych równoległych Udowodnij wcześniej równość dwóch odpowoednio wybranych wysokośći trójkątów ABC i CDA z rysunku Dla trójkata ABC wysokościa bedzie |FB|=|AE| Dla trójkata ACD wysokoscia bedzie |CD| Ale ze wzgledu na to ze czworokąt ACDE jest równoległobokiem to ΔACD jest trójkatem prostokątnym dlatego |CD| to jego wysokośc mamy też ze |CD|=|AE|=|FB| Stąd wysokosći trojkatow sa równe . tak myśle że odległośc dwóch prostych równoległych to odległośc między punktami które leżą na tych prostych i jednocześnie te punkty leżą na prostej prostopadłej do tych prostych równoległych

wredulus_pospolitus: Trochę się czepiam, ale: "Równiez |AE|=|CD| Stąd |OC|=CD| " nie wyjaśniłeś skąd to wiemy.

Z.K: Bo czworokąt ACDE jest równoległobokiem