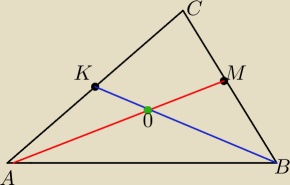
Tróikąt Z.K: W trójkącie ABC punkt K leży na boku AC a punkt M leży na boku BC . Odcinki AK i BM przecinają się w punkcie O Czy może się zdarzyć że punkt O dzieli odcinki AM i BK na polowy ? Mam w odpowiedzi NIE ale dlaczego tak będzie ?

Słoniątko: wykorzystaj :jeżeli w pewnym czworokącie przekątne przecinają się na połowy, to jest on równoległobokiem

Z.K: Rozumiem .Dzięki za podpowiedz

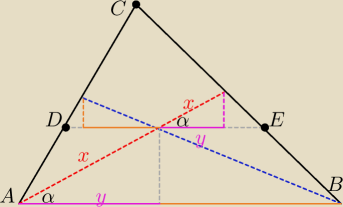
wredulus_pospolitus: albo bez tego faktu, patrzymy. Załóżmy, że jest to możliwe, wtedy (patrz rysunek) 1. prowadzimy równoległą do podstawy, przechodzącą przez punkt przecięcia O. 2. Stąd mamy równość kątów α 3. Skoro mamy równość odcinków x, to z trygonometrii mamy także równość odcinków y. Analogicznie dla drugiej części. Związku z tym |AB| < |DE| Teraz piszemy proporcję z tw. Talesa i wykazujemy sprzeczność. Wniosek: Jest to niemożliwe.

Z.K: wredulus W sumie to zadanie jest z działu o przystawaniu trójkątów Piszą żeby wykorzystac cechę bkb

wredulus_pospolitus: Prędzej bym poszedł kbk (kąt α , przeciwprostokątna, kąt prosty). Bo z tego dopiero mamy równość pozostałych dwóch boków.