Wartośc bezwzględna
Z.K:
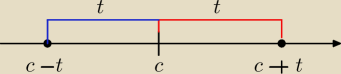
Algebraicznym odpowiednikiem odcinka jest przedział.
Natomiast przedział możemy opisać poprzez jego długość (dokładniej przez połowę jego długości )
i położenie jego środka(za pomocą wartości bezwzglednej ).
|x−c|=t ⇔ x=c−t lub x=c+t
|x−c|<t ⇔ c−t<x<c+t ⇔ x∊(c−t, c+t)
|a−b| −to odległość punktów o współrzędnych a i b
Nierówność
|x−c|<t spełniają liczby z przedziału (c−t,c+t) więc o długości 2t i (c) jest współrzędną
środka tego przedziału
Więc jeśli jest przedział [a,b] gdy a≤b lub przedział [b,a] gdy a≥b to wtedy
Zapiszmy przedział [3.9] za pomocą wartości bezwzględnej
|3−9|=6=2t to t=3
Współrzędna środka przedziału [3,9]
[3,9]=|x−6|≤3
Autor pisze póżniej ze wartość bezwzględna nie nadaje się do opisywania zbiorów
niesymetrycznych (jak np przedziały z jednym końcem czy pojedyncze półproste )
Stąd moje pytanie dlaczego sie nie nadaje?
Dziękuje za odpowiedz.
13 lip 10:45
chichi:
no a czy rozwiązując nierówność typu |x − a| ≤ r,
jestes w stanie uzyskać np przedział typu [e,f) ?
13 lip 12:09
chichi:
przecież w twoim tekście jest podana odpowiedź...
13 lip 12:10
Z.K:
Juz rozumiem . dzięki
13 lip 12:53
 Algebraicznym odpowiednikiem odcinka jest przedział.
Natomiast przedział możemy opisać poprzez jego długość (dokładniej przez połowę jego długości )
i położenie jego środka(za pomocą wartości bezwzglednej ).
|x−c|=t ⇔ x=c−t lub x=c+t
|x−c|<t ⇔ c−t<x<c+t ⇔ x∊(c−t, c+t)
|a−b| −to odległość punktów o współrzędnych a i b
Nierówność
|x−c|<t spełniają liczby z przedziału (c−t,c+t) więc o długości 2t i (c) jest współrzędną
środka tego przedziału
Więc jeśli jest przedział [a,b] gdy a≤b lub przedział [b,a] gdy a≥b to wtedy
Algebraicznym odpowiednikiem odcinka jest przedział.
Natomiast przedział możemy opisać poprzez jego długość (dokładniej przez połowę jego długości )
i położenie jego środka(za pomocą wartości bezwzglednej ).
|x−c|=t ⇔ x=c−t lub x=c+t
|x−c|<t ⇔ c−t<x<c+t ⇔ x∊(c−t, c+t)
|a−b| −to odległość punktów o współrzędnych a i b
Nierówność
|x−c|<t spełniają liczby z przedziału (c−t,c+t) więc o długości 2t i (c) jest współrzędną
środka tego przedziału
Więc jeśli jest przedział [a,b] gdy a≤b lub przedział [b,a] gdy a≥b to wtedy