Wykresy Z.K:

	1
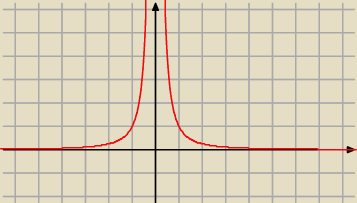
Jak zachowują sie funkcje f(x)=		i g(x)=U[1}{x2} gdy x zbliża sie z którejs strony do
	|x|

zera ? Co się dzieje z wartościami tych funkcji a co z ich wykresami gdy x dąży do +∞ albo gdy dązy do −∞

	1
Wykresy obu funkcji sa prawie takie same (dlatego na rysunku jest g(x)=
	x2

zarówno f(x) i g(x) 1) dąży do +∞ gdy x dąży do zera z prawej strony 2) dąży do +∞ gdy x dąży do zera z lewej strony 3) wartości tych funkcji dążą do 0 gdy x dąży do do +∞ albo gdy dąży do −∞ Natomiast wykresy obu funkcji zbliżają się do osi OX Jest ok? Tak ?

Z.K: Dalej do tego ćwiczenia jest tak . Opisaną powyżej sytuację można sformalizować . Mówimy ze funkcja dąży do plus nieskończoności gdy x dąży do x₀ z prawej strony jeżeli dla dowolnej liczby a istnieje δ>0 taka że f(x)>a dla każdego x∊(x₀, x₀+δ) Zapisujemy to jako lim f(x)=+∞ x→x₀⁺ Mówimy tez że funkcja f ma w x₀ prawostronną granicę niewłaściwą +∞. O liczbie a należy myśleć że jest dowolnie duża .Istnienie δ oznacza istnienie (choćby nawet bardzo małego ) przedziału otwartego z lewym końcem x₀ i takiego że część wykresu funkcji f mu odpowiadająca leży powyżej prostej y=a Mówimy że prawostronna granicą funkcji f w punkcie x₀ jest (−∞) jeżeli dla każdego a istnieje δ>0 taka że f(x)>a dla x∊(x₀,x₀+δ)piszemy wtedy lim f(x)=−∞ x→x₀⁻ Analogicznie określamy lewostronna granice niewłaściwą (+∞) w x₀ czyli dążenie funkcji do +∞ z lewej strony x₀ co zapisujemy lim f(x)=+∞ x→x₀⁻ gdy dla dowolnego a istnieje δ>0 taka że f(x)>a dla każdego x∊(x₀−δ,x₀) .wtedy interesują nas x bliskie x₀ ale mniejsze od niego x,x₀. Mówimy że lewostronną granicą niewłaściwą funkcji f w punkcie x₀ jest (−∞) jeżeli dla każdego a istnieje δ>0 taka że f(x)<a dla x∊(x₀−δ.x₀) piszemy wtedy lim f(x)=−∞ x→x₀⁻

	1		1
Jeśli (tak było np dla f(x)=		) i także dla g(x)=
	x2		|x|

lim f(x)=+∞ i limf(x)=+∞ x→x₀⁻ x→x₀⁺ to mówimy ze funkcja f(x) ma w x₀ granice niewłaściwą +∞ i piszemy lim f(x)=+∞ x→x₀ Analogicznie lim f(x)=−∞ i lim f(x)=−∞ oznacza ze funkcja f ma w x₀ granice niewłaściwa (−∞) x→x+0⁻ x→x₀⁺ więc lim f(x)=−∞ x→x₀ Teraz posługując sie tym sprawdzić jakie granice niewłaściwe maja funkcje

	1
f(x)=		+1
	x

	1
g(x)=		−100
	5x

	1
h(x)=		+x2
	x

w punkcie x₀=0