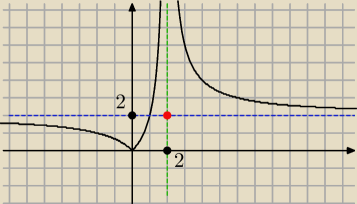
Wykresy i granice Z.K: Na rysunku jest wykres funkcji

	4
y=|2+		|
	x−2

Jak zachowuje sie nasza funkcja przy x dążącym do 2 ? Przy x dążącym do 2 z prawej strony i przy x dążącym do 2 z lewej strony dąży ona do +∞ Natomiast gdy x dąży do [0,−∞) to wartości tej funkcji dążą do (−∞) czy do 2 ? Chyba do 2 . Teraz także pytanie . jak zachowuje sie funkcja gdy x dązy [0,∞) Widac ze dla x∊[0,2) dązy do (+∞) a dla (2,∞) dąży do 2 Więc jak mam zapisac jak zachowuje sie funkcja dla x dążącym do (+∞)? Granice odczytujemy z wykresów na razie dziękuje za odpowiedz .

chichi: takie brednie wypisujesz, że szok... jak x może dążyć do zbioru funkcja ma nieskończenie wiele granic punktowych zarówno dla x zbiegającego do 2 granica istnieje i jest niewlasciwa, wynosi +∞. lim_x→∞f(x) = 2, a jak bys mial zapisac?

Z.K: OK Do wytłumaczenia dla ucznia klasy 2 który zaczyna dopiero funkcje wymierne i ich wykresy Natomiast np [0 2) nie potraktowałem z klasy 1 jako zbiór tylko przedział

wredulus_pospolitus: zastanwiamy się 'do czego dąży' funkcja w kontekście: 1. +/− ∞ (czyli co się dzieje z wykresem funkcji poza kartką) 2. w punktach nieciągłości funkcji / wypadających z dziedziny (u nas jest to x = 2) Nie mówimy, że funkcja na przedziale [a,+∞) dąży do wartości b ... tylko że dla x dążącego do +∞ funkcja dąży do b.

wredulus_pospolitus: tak więc mamy pytanie: lim_{x−> −∞} f(x) = lim_{x−> 2⁻} f(x) = lim_{x−> 2⁺} f(x) = lim_{x−> +∞} f(x) = Możemy rozmawiać funkcji rozpatrując jej przedział w kontekście jej (np.) monotoniczności. I de facto Ty to robiłeś bo sobie podzieliłeś na przedziały gdzie funkcja jest monotoniczna. I jeszcze taka uwaga −−−> [0 ; −∞) <−−−− absolutnie nie zapisujemy w ten sposób przedziałów Winno być (−∞ ; 0]

chichi: "Natomiast np [0 2) nie potraktowałem z klasy 1 jako zbiór tylko przedział" no widzisz, pojęcie zbioru miałeś w 1 klasie, a go wciąż nie rozumiesz, dlaczego więc jesteś tak daleko skoro z tyłu takie braki? o drugiej uwadze co do zapisu wspomniał wredny [0,2) = {x∊ℝ : 0 ≤ x < 2}

Z.K: wredulus popatrzyłem tak i zapisałem