Wymierne Z.K: Dzień dobry. Mam takie ćwiczenie w podręczniku . Funkcja f(x) spełnia (dla każdego x) równość f(|x|)=|f(x)|. Czy tak jest dla każdej funkcji? Opisz geometryczny sens tej równośći . Znajdz jeszcze parę funkcji spełniających ją . Ogólnie jestem w tym momencie na funkcjach wymiernych i poprzednie ćwiczenie było takie Narysuj wykresy funkcji

	1
a) y=−
	x

	1
b) y=
	|x|

	1
c) y=−
	|x|

Która z narysowanych krzywych jest hiperbolą ?

	1
Hiperbolą jest tylko krzywa y=−
	x

wredulus_pospolitus: 1. zauważmy, że f(|x|) = f(x) możemy także rozumieć jako f(−x) = f(x) co jest warunkiem parzystości funkcji. 2. warunek, że f(|x|) = |f(x)| oznacza, że f(x) ≥ 0 dla dowolnego x∊D_f

Z.K: Dzięki. Czytam dalej

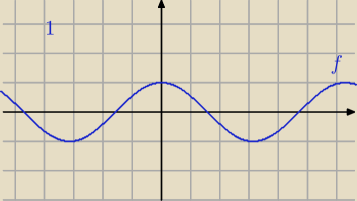
Mila: Przykład dla f(|x|)=|f(x)|. 1) f(x)=cos(x)

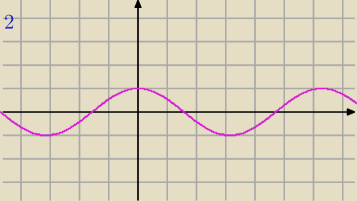
Mila: 2) f(|x|)=cos(|x|)=cos(−x)

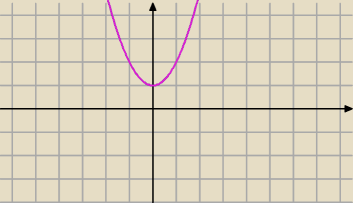
Mila: 1) cos(|x|)≠|cos(x)| 2) g(x)= x²+1 g(|x|)=|g(x)|

Z.K: Dziękuje Milu i pozdrawiam Jest to ćwiczenie nr 15 z Anusiaka (klasa 2) z funkcji wymiernej . Natomiast po ćwiczeniu nr 18 (u mnie strona 78) jest tam napisane tak Przypominamy ze wykres funkcji y=f(x−r)+s(y−s=f(x−r)) jest wynikiem przesunięcia wykresu y=f(x) o wektor [r,s] Wiem jak przesuwać wykres o wektor ale nie bardzo rozumiem ten czerwony zapis Czy możesz to mi wytłumaczyć w miare możliwości .Dziękuje

Mila: Dobry wieczór. Jutro spojrzę. Upał na mnie źle działa. Jak Ty znosisz takie temperatury?

Z.K: Milu Poczekam. Staram sie nie wychodzić dużo w ten upał.

wredulus_pospolitus: Miluś ... f(x) = cosx to słaby przykład gdyż: niech x = π nie spełnia warunku f(|π|) = |cosπ|

Mila: Witam miło Właśnie to napisałam 21: 51. To był przykład funkcji parzystej.

wredulus_pospolitus: ale już f(x) = cosx + 1 bym pasował

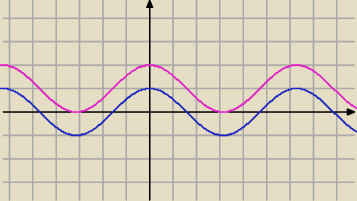
Mila: Wszystko zgodnie z tym co napisałeś 20:10