Okręgi Z.K: Trzy równe okręgi parami zewnętrznie styczne ograniczają trójkąt krzywoliniowy Obliczyć pole powierzchni tego trójkąta wiedząc że promień okręgu opisanego na figurze utworzonej z wymienionych trzech okręgów równy jest R

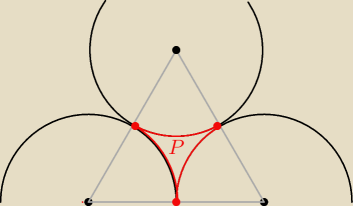
wredulus_pospolitus: Zauważ, że wierzchołki tego trójkąta krzywoliniowego tworzą trójkąt równoboczny o boku równym ¹/₂ szarego okręgu równobocznego. W takim razie, na szarym trójkącie moglibyśmy opisać okrąg o promieniu 2R. Związku z tym, bok tegoż szarego trójkąta wynosi a = 2√3R. Czyli r_{trzech okręgów} = √3R

	a2√3		3*60		3
Stąd P =		−		*πr2 = (3√3 −		π)*R2
	4		360		2

O ile nigdzie się nie walnąłem w przekształcając/podstawiając w pamięci.

Z.K: Mam tylko odpowiedzi

	3(2√3−π)R2
Tutaj S=
	2(7+4√3)

Dziękuje .

Mila: Jeżeli promienie okręgów ozn. r to promień okręgu opisanego na tych 3 okręgach jest równy:

	2+√3
R=		r
	√3

	R√3
r=
	2+√3

Licz dalej sam P=P_sz.Δ−3 wycinki koła o promieniu r wyjdzie dobrze.

Z.K: Dzień dobry Milu Policzę to póżniej gdyż teraz mam wahania cukru i zle się czuję . Odpuszczam na razie następne zadania z wykresów

wredulus_pospolitus: ach ... znowu nie doczytałem ja przyjąłem okrąg który był opisany na tym trójkąciku krzywoliniowym

Mila: Rysunek ładny, skorzystałam z niego