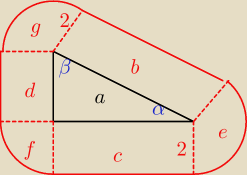
 1)
5,12,13 <−−− jest to drugi (po 3,4,5) trójkąt prostokątny o całkowitych długościach boków −−−
warto to zapamiętać.
2) Tak więc −−− tenże trójkąt jest trójkątem prostokątnym. związku Pole 'a' obliczysz bez
problemu
3) pola b,c,d są to po prostu pola prostokątów o odpowiednich bokach
4) natomiast pola e,f,g są polami wycinków okręgów o promieniu r = 2
jakich wycinków się zapytasz
zauważ, że to będą odpowiednio:
dla e: 360o − α − 90o − 90o = 180o − α
dla f: to będzie po prostu 90o
dla g: 360o − β − 90o − 90o = 180o − β
czyli w sumie te trzy pola są 'wycinkiem' okręgu o kącie:
180o − α + 180o − β + 90o = 360o − (α+β) + 90o
A ile wynosi (zawsze w trójkącie prostokątnym) α+β
1)
5,12,13 <−−− jest to drugi (po 3,4,5) trójkąt prostokątny o całkowitych długościach boków −−−
warto to zapamiętać.
2) Tak więc −−− tenże trójkąt jest trójkątem prostokątnym. związku Pole 'a' obliczysz bez
problemu
3) pola b,c,d są to po prostu pola prostokątów o odpowiednich bokach
4) natomiast pola e,f,g są polami wycinków okręgów o promieniu r = 2
jakich wycinków się zapytasz
zauważ, że to będą odpowiednio:
dla e: 360o − α − 90o − 90o = 180o − α
dla f: to będzie po prostu 90o
dla g: 360o − β − 90o − 90o = 180o − β
czyli w sumie te trzy pola są 'wycinkiem' okręgu o kącie:
180o − α + 180o − β + 90o = 360o − (α+β) + 90o
A ile wynosi (zawsze w trójkącie prostokątnym) α+β  Więc jaki będzie ostatecznie kąt 'wycinka' okręgu'
Więc jaki będzie ostatecznie kąt 'wycinka' okręgu'  Mam nadzieję, że z samymi obliczeniami już sobie poradzisz.
Mam nadzieję, że z samymi obliczeniami już sobie poradzisz.

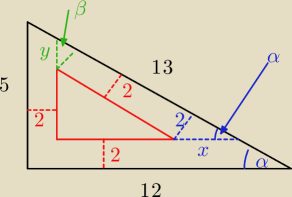 z podobieństwa trójkątów:
niebieski
z podobieństwa trójkątów:
niebieski
| x | 13 | 26 | |||
= | −−−> x = | ||||
| 2 | 5 | 5 |

 A odległość tego punktu to do którego punktu będzie 2 cm?
A odległość tego punktu to do którego punktu będzie 2 cm?
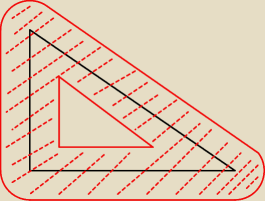 żeby nie było wątpliwości ... czarny −−− wyjściowy trójkąt o bokach 50,120,130
czerwone zakreskowane pole to pole którego szukasz
które łatwiej policzyć jako
pole czarnego trójkąta (50,120,130) − pole czerwonego trójkąt (o którym mówiłem w ostatnim
poście) + pole 'a,b,c,d,e,f' (o których wspominałem w pierwszym poście)
żeby nie było wątpliwości ... czarny −−− wyjściowy trójkąt o bokach 50,120,130
czerwone zakreskowane pole to pole którego szukasz
które łatwiej policzyć jako
pole czarnego trójkąta (50,120,130) − pole czerwonego trójkąt (o którym mówiłem w ostatnim
poście) + pole 'a,b,c,d,e,f' (o których wspominałem w pierwszym poście)
 Nie rozumiem tylko czemu ten wewnętrzy trójkąt nie jest zaokrąglany bo ta odległość nie ma
wtedy 2 cm tylko wg mnie więcej.
Nie rozumiem tylko czemu ten wewnętrzy trójkąt nie jest zaokrąglany bo ta odległość nie ma
wtedy 2 cm tylko wg mnie więcej.
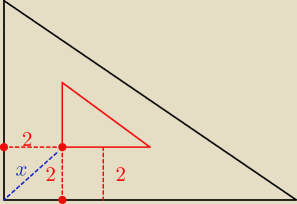 te dwa punkty z wyjściowego (czarnego) trójkąta mają dokładnie 2cm do tegoż punktu czerwonego
(mniejszego) trójkąta.
x jest oczywiście > 2 , a dokładniej − wynosi 2√2 cm
te dwa punkty z wyjściowego (czarnego) trójkąta mają dokładnie 2cm do tegoż punktu czerwonego
(mniejszego) trójkąta.
x jest oczywiście > 2 , a dokładniej − wynosi 2√2 cm
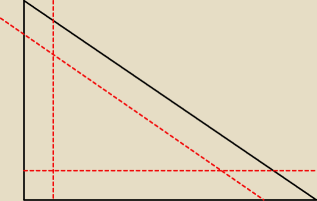 możesz na to popatrzeć w ten sposób.
Rysujesz wyjściowy trójkąt (czarny).
Następnie rysujesz trzy równoległe do boków (o tej samej długości), oddalone o tychże boków o
2cm.
W ten sposób został wyznaczony wewnętrzny trójkąt
możesz na to popatrzeć w ten sposób.
Rysujesz wyjściowy trójkąt (czarny).
Następnie rysujesz trzy równoległe do boków (o tej samej długości), oddalone o tychże boków o
2cm.
W ten sposób został wyznaczony wewnętrzny trójkąt
| y | 130 | ||
= | (y to przeciwprostokątna) | ||
| 2 | 120 |