trójkat Przew: Niech ABC będzie trójkątem, w którym ABC= 30°. ACB=15°. AB=12. Wybieramy punkt D na BC taki, że DAC=30°. Jeśli O jest środkiem okręgu przechodzącego przez A, B i C, wyznacz długość OD

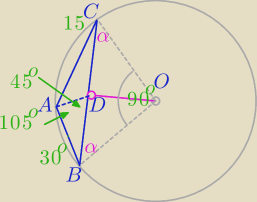
ite: |<ABC|=30^o, |<ACB|=15^o, |AB|=12, |<DAC|=30°, |<ODB|=90° wtedy |<CAB|=135^o więc oparty na tym samym łuku kąt wklęsły |<COB|=270^o zatem oparty na łuku CAB kąt wypukły |<COB|=90^o ΔCBO jest równoramienny → |<DOB|=45^o,

	|BO|
z tego wynika że również ΔDBO jest równoramienny → |DO|=
	√2

	|AB|
2R=		=12√2 // tw.sinusów
	sin 45o

|BO|=R=6√2 |DO|=6

ite: niestety wynik do poprawienia

	|AB|
2R=
	sin 15o

Mila: ΔDBO jest równoramienny jeśli D jest środkiem BC ( oczywiście tu jest), czy nie trzeba tego wykazać? Czy coś przeoczyłam w Twoim rozwiązaniu? Pozdrawiam