Mi Ka:
cos
2x+sin2x=sinx
cos
2y+sin2y−siny=0
| | 3 | | 1 | |
cos2y+2cos |
| y*sin |
| y=0 |
| | 2 | | 2 | |
Nie wiem jaki wspolny czynnik przed nawias dac
albo tak
(1−sin
2y)+2sinycosy−siny=0
(1−sin
2y)+siny(2cosy−1)=0
Teraz pytanie
czy tutaj moge zapisac ze to będzie równe zero gdy
(1−sin
2y)=0 i siny(2cosy−1)=0 ?
Jesli tak to
| | π | | 3π | |
sin2y=1 y= |
| lub y= |
| |
| | 2 | | 2 | |
siny(2cosy−1)=0
siny=0 y=0 (odpada ze względu na przedział ) lub y=π(dobry
| | 1 | | π | | 5π | |
lub 2cosy−1=0 cosy= |
| y= |
| lub y= |
| |
| | 2 | | 3 | | 3 | |
Po podstawieniu do równania
cos
2y+sin(2y)=siny zaden z nich nie spełnia tego równania
Zrobie podstawienie
| | 2t | | 1−t2 | | 1 | | 1 | |
siny= |
| cosy= |
| t=tg |
| y i tg |
| y y≠(2k+1)π |
| | 1+t2 | | 1+t2 | | 2 | | 2 | |
cos
2y+2siny*cosy−siny=0
| | 1−t2 | | 2t | | 1−t2 | | 2t | |
( |
| )2+2* |
| * |
| − |
| =0 |
| | 1+t2 | | 1+t2 | | 1+t2 | | 1+t2 | |
po uporzadkowaniu
| t4−6t3−2t2+2t+1 | |
| =0 |
| (1+t2)2 | |
t
4−6t
3−2t
2+2t+1=0
całowitych pierwiastków brak więc wole wykres zrobic niz rozwiązywac to równanie
Ty możesz spróbowac .
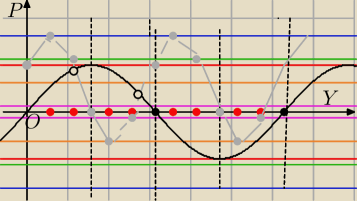 szary f(y)=cos2x+sin(2x)
czarny f(y)=siny
W przedziale (0,2π) równanie to ma dwa rozwiązania rzeczywiste
szary f(y)=cos2x+sin(2x)
czarny f(y)=siny
W przedziale (0,2π) równanie to ma dwa rozwiązania rzeczywiste