pięciokat ulrajsk: W pięciokącie ABCDE AB=BC, CD=DE; kąt ABC=120 i kat CDE=60 oraz BD=2. Oblicz pole pięciokąta.

Min.Edukacji: Narysuj go ładnie, to zobaczysz rozwiązanie.

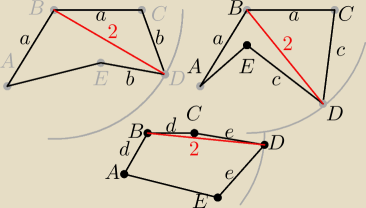
wredulus_pospolitus: Niestety, treść zadania nie wskazuje nam co to za 5−ciokąt. Każdy z tych trzech powyżej pięciokątów spełnia warunki zadania. Ale czy mają jednakowe pole? Nie wydaje mi się (ale oczywiście mogę się mylić).

wredulus_pospolitus: Heh ... ale faktycznie ... pole może być stałe ... ciekawe.

wredulus_pospolitus: Kurczę ... wyszło z tego fajne zadanie ... gdy się przy okazji udowodni, że pole tego pięciokąta jest stałe (bez względu na pozostałe boki i kąty) i jest równe polu odpowiedniego trapezu bądź równoległoboku. Sam dowód równości pól zrobiłem dla równoległoboku, ale później można wykazać, że tenże równoległobok ma równe pole z trapezem, a nawet z odpowiednim trójkątem równobocznym..

ulrajsk: pole jest stałe i wychodzi √3

wredulus_pospolitus: tak ... pytanie czy udowodniłeś to, źe pole jest stałe

: Wynik P=√3 jest poprawny przy założeniu, iż kąty: ''kąt ABC=120 i kat CDE=60'' są kątami wewnętrznymi pięciokąta i wyrażonymi w stopniach, oraz wewnętrzny kąt BCD jest niemniejszy od kąta prostego i niewiększy od półpełnego. Górny prawy pięciokąt narysowany przez .. takiego pola nie ma.

: Wynik P=√3 jest poprawny przy założeniu, iż kąty: ''kąt ABC=120 i kat CDE=60'' są kątami wewnętrznymi pięciokąta i wyrażonymi w stopniach, oraz wewnętrzny kąt BCD jest niemniejszy od kąta prostego i niewiększy od półpełnego. Górny prawy pięciokąt narysowany przez .. takiego pola nie ma.

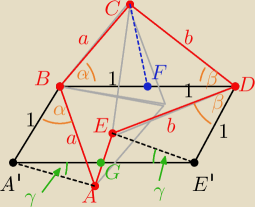
wredulus_pospolitus: @: trochę się pośpieszyłeś z tym, że prawy górny ma inne pole niż √3. Coś czuję, że mało przejrzysty będzie to rysunek. Więc mały opis: Krok 1: Rysuję równoległobok A'BDE' o bokach 2x1 (gdzie |BD| = 2) i ∡E'A'B = 60^o Krok 2: Szkicuję na nim pięciokąt ABCDE Krok 3: Zaznaczam połowę odcinka BD, punkt F Krok 4: ΔDFC przystaje do ΔDE'E (cecha bkb) Krok 5: ΔBFC przystaje do ΔBA'A (cecha bkb) Krok 6: Związku z tym pola odpowiadających trójkątów są sobie równe. Krok 7: Związku z tym pole pięciokąta ABCDE jest równe polu sześciokąta AA'BDE'E Krok 8: Pozostaje wykazanie, że P{ΔA'AG) = P_ΔE'EG (czyli, że są to trójkąty przystające) Krok 9: |A'A| = |FC| = |E'E| Krok 10: Oczywistą oczywistością jest równość ∡A'GA = ∡E'GE Krok 11: Z przystawania ΔBFC i ΔBA'A mamy: ∡AA'B = ∡CFB Krok 12: Związku z tym kąt γ = ∡A'AB = ∡CFB − 60^o Krok 13: Z przystawania ΔDFC i ΔDE'E mamy: ∡EE'D = ∡CFD = 180^o − ∡CFB Krok 14: Związku z tym ∡GE'E = 120^o − ∡EE'D = 120^o − (180^o − ∡CFB) = ∡CFB − 60^o = γ Krok 15: Tak więc, ΔA'AG przystaje do ΔE'EG (cecha bkk) Krok 16: Wniosek: P_AA'BDE'E = P_{A'BDE') = 2*1*sin60^o = √3

wredulus_pospolitus: Pragnę zauważyć, że powyższy rysunek (i procedura postępowania) jest niezależna od kątów α i β jak również długości boków a i b w ΔBDC. Związku z tym, jest to prawda dla DOWOLNEGO ∡DEA >180^o I dla wyjaśnienia −−− skąd przystawanie w krok 5: ∡A'BD = 120^o (kąt w równoległoboku) = ∡A'BA + ∡ABD ∡ABC = 120^o (dane z zadania) = ∡ABD + ∡DBC Z tego: ∡A'BA = ∡DBC = α Analogicznie z kątem β (krok 4)

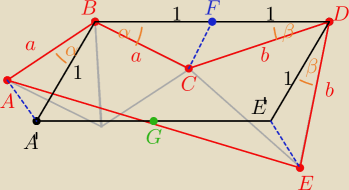
wredulus_pospolitus: Co do warunku, że ∡BCD ∊ (90^o ; 180^o) także nie mogę się zgodzić. Kąt może być mniejszy od 90^o, co wykazałem już w powyższym. A co do być kątem większym od 180^o, to masz powyższy rysunek. Robimy to samo. Mamy analogiczne przystawanie trójkątów i do wykazania P_ΔA'AG = P_ΔE'EG Co także wykazujemy poprzez kąty: ∡GA'A = 60^o + ∡AA'B = 60^o + ∡BFC = = 60^o + 180^o − ∡CFD = 240^o − ∡EE'D = 240^o − (240^o − ∡GE'E) = ∡GE'E

Mila: Podziwiam wytrwałość.