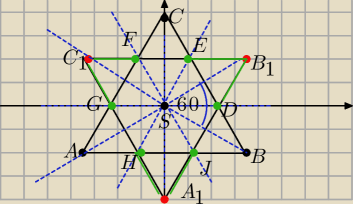
Niech T oznacza dany trójkąt równoboczny o środku ciężkości w punkcie S i boku mającym długość
a
T' jego obraz w obrocie płaszczyzny zawierającej T dookoła punktu O o kąt 60 o .
narysować figure F=TUT'.
Obliczyć jej pole powierzchni . Ile symetrii ma figura F ?
Narysowałem trójkąt równoboczny w układzie współrzędnych gdzie jego środek jest środkiem
ciężkości trójkąta T.
PP =PABC+PEDB1+PGFC1+PHJA1
| a2√3 | ||
PABC | ||
| 4 |
| 1 | ||
Trójkąty EDB1, GFC1, HJA1 to trójkaty równoboczne o bokach długości | a | |
| 3 |
| a2√3 | 19a2√3 | a2√3 | a2√3 | |||||
PP= | +3* | = | +3* | = | ||||
| 4 | 4 | 4 | 36 |
| a2√3 | a2√3 | 4a2√3 | a2√3 | |||||
= | + | = | = | |||||
| 4 | 12 | 12 | 3 |
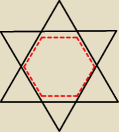1. zauważ, ów gwiazda składa się z:
a. 6−ciokątu foremnego (który składa się z 6x trójkąt równoboczny)
b. 6x trójkąt równoboczny
| a | ||
bok małego trójkąta równy jest | ||
| 3 |
| a2√3 | a2√3 | |||
więc Pgwiazdy = 12* | = | <−−− trochę mniej zabawy. nie sądzisz | ||
| 9*4 | 3 |
