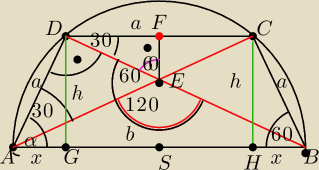
trapez Mi Ka: Kazdy z trzech boków trapezu ma długośc 1 Miara kąta ,w którego wnętrzu leży jedna z podstaw trapezu a którego ramiona leża na prostych zawierających przekątne trapezu jest równa 120^o.

	1
czy pole tego trapezu jest większe od 2−		?
	√2

a=1 AB=b Trapez jest równoramienny wiec można na nim opisać okrąg Punkty C i D leżą na okręgu więc kąt ADB i kąt ACB ma miarę 90^o Kąt α=60^o b=a+2x W trójkącie prostokatnym AGD

	x
cos60o=
	a

	1
x=cos60o*a=
	2

	h
sin60o=
	a

	√3
h=sin60o*a=
	2

	a+b
P=		*h
	2

	1   1+2*   2		√3		√3
P=		*		=		≈0,866
	2		2		2

	1		2−√2
2−		=		=0,293
	√2		2

√3		1
	>2−
2		√2

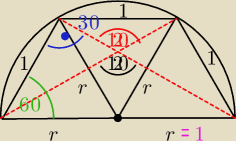wredulus_pospolitus: coś nie tak Ci wyszło ... ale do rzeczy. Lecimy: 1. podane dane z zadania 2. z tw. o kąta przystających 3. suma kątów w trójkącie równoramiennym oraz tw. o kącie wpisanym i środkowym 4. z sumy kątów trapezu 5. nasze trójkąty równoramienne stają się równobocznymi

	12√3		3√3
W efekcie Ptrapezu = 3*PΔ = 3*		=		<−−− i dlatego mówię, że coś
	4		4

nie tak Ci wyszło

wredulus_pospolitus: już widzę −−−> do pola trapezu zrobiłeś b = 2*x = |AG| + |HB| ... ... a powinieneś brać b = 2x + a = |AG| + |GH| + |HB|

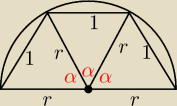wredulus_pospolitus: a teraz jeszcze łatwiejsze dojście do tegoż faktu (jako, że się rozbudziłem w końcu): 1. Zauważamy, że mamy 3 przystające trójkąty równoramienne (cecha bbb)

	180
2.		= α −> są równoboczne −> r = 1
	3

	3√3
3. Ptrapezu = 3*PΔ =
	4

Mi Ka: No tak . A cały czas myślałem o tym żeby te jedynke dodac do tych 2x Znowy .W nocy sie śpi

Mi Ka: Oczywiście dzięki za pomoc