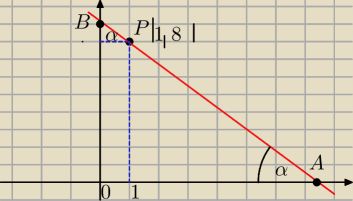
Współczynnik kierunkowy Mi Ka: Znajdz współczynnik kierunkowy prostej przechodzącej przez punkt P(1,8) i wyznaczającej w pierwszej ćwiartce układu współrzędnych odcinek o najmniejszej długości. α−kąt nachylenia prostej AB do osi OX Mamy wtedy tgα=−m AB=AP+PB

	8		8
sinα=		AP=
	AP		sinα

	1		1
cosα=		PB=
	PB		cosα

	8		1
AB=		+
	sinα		cosα

	8		1		π
Obliczamy wartośc α dla której funkcja f(α)=		+		0<α<
	sinα		cosα		2

ma minimum

	−8cosα		sinα		−8cos3α+sin3α
f'(α)=		+		=		=
	sin2α		cos2α		sin2cos2

	sin3α−8cos3α
=
	sin2α*cos2α

sin³α−8cos³α=0 sinα*sin²α−8cosα*cos²α=0 sinα(1−cos²α)−8cosα(1−sin²α)=0 Tutaj troche sie zaciąlem

Mi Ka: W książce mam tylko tak

	−8cosα		sinα
f'(α)=		+		(do tej postaci udało mi sie doprowadzic i potem
	sin2		cos2α

	tg3α−8
=		(tego nie wiem jak zrobic wiec probowałem do wspolnego mianownika i
	tgαsinα

licznik przyrownac do zera

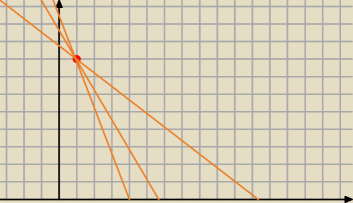wredulus_pospolitus: całkowicie z innej strony podejdę do zadania (bo nie lubię się babrać w funkcjach trygonometrycznych). 0. f(x) = a(x−1) + 8 <−−− ogólny wzór każdej prostej przechodzącej przez punkt (1,8) 1. wyciągamy oczywisty wniosek, że a < 0

	8
2. miejsca przecięcia tejże funkcji z osiami OX i OY to (1 −		, 0) oraz (0; 8−a)
	a

	8
3. szukamy minimum funkcji g(a) = x02 + (f(0))2 = (1 −		)2 + (8−a)2 =
	a

	(8−a)2		1
=		+ (8−a)2 = (8−a)2*(1+		)
	a2		a2

	a2+1		2
4. g'(a) = 2(8−a)*(		)*(−1) + (8−a)2*(−		)* =
	a2		a3

	a2 + 1		(8−a)		a3 + 8
= −2(8−a)* [		+		] = −2(8−a)*
	a2		a3		a3

5. g'(a) = 0 −−−> a = 8 (odpada) lub a = −2 tgα = −2 −−−> α =

wredulus_pospolitus: a w ogóle nie wnikając w Twoje obliczenia (wybacz ... nie lubię się babrać w czymś takim −−− ale to już wspomniałem)

−8cosα		sinα		−8		tgα
	+		=		+		=
sin2α		cos2α		tgα*sinα		cosα

	−8		tgα *sinα * tgα
=		+		=
	tgα*sinα		tgα*sinα *cosα

	−8		tg3α
=		+
	tgα*sinα		tgαsinα

Mi Ka: Dziekuje Ci No tak . Jednak noc jest od spania