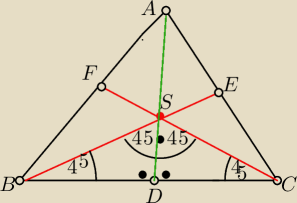
Srodkowe trójkata Mi Ka: W trójkącie ABC gdzie AB=AC środkowe poprowadzone z wierzchołków B i C są prostopadłe. Wyznaczyć miarę kąta BAC BE i CF i AD − środkowe trójkata ABC BE⊥FC BE=FC Srodkowe BC i FC są równe i prostopadłe wiec trójkąt BSC jest trójkątem prostokątnym równoramiennym |BS|=|SC|

	1
SD=		|BC|=|BD|=|DC|
	2

	1
|SD|=		|AD|
	3

|AD|=3|SD|=3|BD|=3|DC| |BD|=|DC|=x |AD|=3x

	x		1
tg∡BAD|=		=
	3x		3

	1
∡|BAC|=2∡|BAD|=2*tg
	3

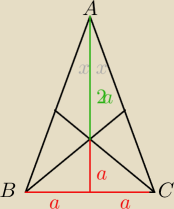SAIzou: Środkowe przecinają się w jednym punkcie w stosunku 1:2

	a		1
tgx=		=
	3a		3

	2tgx		1   2*   3		2		9		3
tg(2x) =		=		=		*		=
	1−tg2x		1   1−( )2   3		3		8		4

2x ~ 37°

Mi Ka: No tak. dzięki Pomyliło mi sie .zamiast tg(2α) to policzyłem 2tgα.