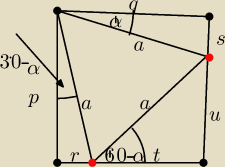
Prostokąt i trójkąt rownoboczny Mi Ka: Trójkąt równoboczny został wpisany w prostokąt nie będący kwadratem w sposób przedstawiony na rysunku Udowodnić że p*r+q*s=t*u Z rysunku wynika że p,r,t,u,s,q, możemy uzależnić od boku (a) trójkąta równobocznego

	p
cos(30o−α)=		p=a*cos(30o−α)
	a

	r
sin(30o−α)=		r=a*sin(300−α)
	a

	t
cos(60o−α)=		t=a*cos(60o−α)
	a

	u
sin(60o−α)=		u=a*sin(60o−α)
	a

	q
cosα=		q=a*cosα
	a

	s
sinα=		s=a*sinα
	a

p*r+q*s=t*u [(a*cos(30^o−α))*(a*sin(30^o−α))]+[(a*cosα)*(a*sinα)]=[(a*cos(60^o−α))*(a*sin(6o^o−α))] L=a²*cos(30^o−α)*sin(30^o−α)+a²*cosα*sinα= =a²[cos(30^o−α)*sin30^o−α)+cosα*sinα]=

	1
=		a2[sin(60o−2α)+sin2α]=a2*sin30o*cos(30o−2α)
	2

P=a*cos(60^o−α)*a*sin(60^o−α)=a²[cos(60^o−α)*sin(60^o−α)]=

	1
=		a2*sin(120o−2α)
	2

sin(120^o−2α)=sin[90^o+(30⁰−2α)]=cos(30^o−2α)

1
	=sin30o
2

1
	*a2*sin(120o−2α)=a2*sin30o*cos(30o−2α)
2

L=P

wredulus_pospolitus: z innej perspektywy: q = a*cosα p = a*cos(30−α) t = a*cos(60−α) u = a*sin(60−α) i teraz: p*r+q*s=t*u ⇔ P_Δtu = P_Δpr + P_Δqs dla ułatwienia równanie pól mnożę przez 4 4*Prawa = 2pasinα + 2qasin(30−α) = 2a²sinαcosα + 2a²sin(30−α)cos(30−α) =

	60		4α − 60
= a2( sin(2α) + sin(60 − 2α)) = a2*2sin		*cos		= a2cos(2α − 30) =
	2		2

= a²sin(90 − (2α − 30)) = a²sin(120 − 2α) = 2a²sin(60−α)cos(60−α) = 2t*u = 4*Lewa c.n.w.

Mi Ka: Witam wredulus i dzięki